Améliorations possibles?

Archives Sakia
13

Ca ne me semble pas clair, c’est peut-être juste, mais je vois mal la démonstration.

Etant donné que le nombre de DU produits à t alors x(t) = 1/c*[1-exp(-ct)], et nous cherchons “t” tel que x(t) = 2x(t0) (en posant x = x(t0) soit exp(-ct0) = 1 - cx ou encore t0 = -1/c ln(1-cx)) soit :

1/c*[1-exp(-ct)] = 2/c*[1-exp(-ct0)] => t = - 1/c ln(2 exp(-ct0) - 1) = -1/c ln(1-2cx) et donc pour connaître t-t0 :

t-t0 = -1/c ln(1-2cx) - (-1/c ln(1-cx)))
t-t0 = 1/c*(ln(1-cx) - ln(1-2cx)

Ce qui ressemble exactement à ta solution, mais avec “cx” à la place de “x” tout seul, la solution impliquant que x doit être strictement inférieur à 1/2 1/c. Ceci étant une question de notation, expliqué par le fait que tu as choisi de donner à x une valeur “fraction de c”, et pas un “nombre de DU” exprimé en fonction de “c”, pure question de convention.

A noter toutefois que pour être complet cela ne suffit pas ! Car il faut que la solution soit aussi inférieure à l’espérance de vie pour “t” pour prétendre connaître le cas général (quoique pour un individu particulier on puisse aller au delà de “ev”, il nous faut tout de même garder en tête la limite moyenne de vie et connaître les solutions qui s’y rapportent) Donc il faut poursuivre :

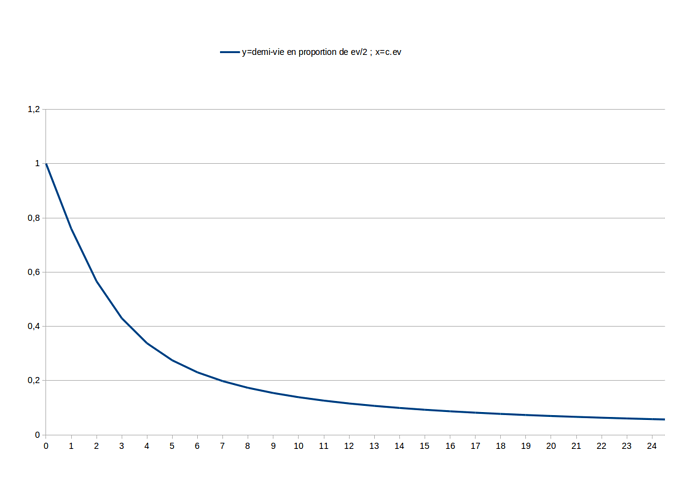
t = -1/c ln(1-2cx) < ev => x < 1/2 1/c [1 - exp(- c ev)]

Qui est une condition plus forte que la précédente. Par ailleurs si on note que c = ln(ev/2) / (ev/2), alors cela se simplifie encore par :

x < 1/2 1/c [1 - exp( - 2 ln(ev/2)] soit x < 1/2 1/c [1 - 1/(ev/2)²]

Il s’ensuit qu’un individu ayant déjà produit “x” DU verra sa production doubler au bout de :

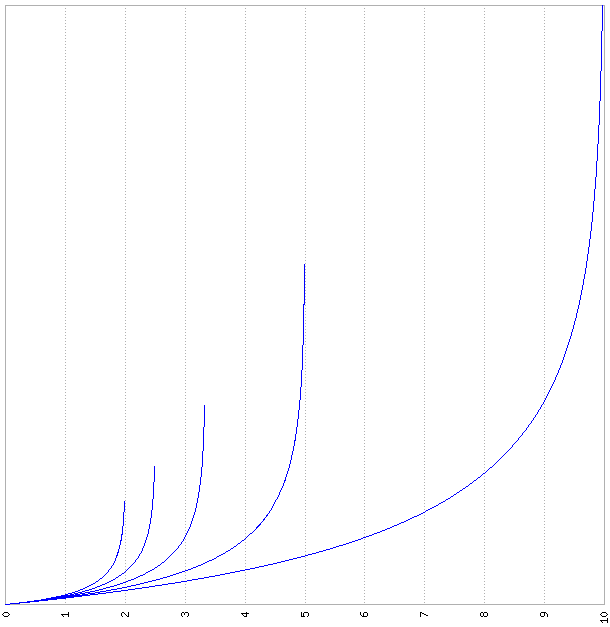
t-t0 = 1/c*[ln(1-cx) - ln(1-2cx)] = 1/c ln[(1-cx)/(1-2cx)]

Sous condition que x < 1/2 1/c [1 - 1/(ev/2)²] pour des individus de durée d’espérance de vie moyenne “ev”, avec c = ln(ev/2)/(ev/2)

Il n’y a plus qu’à réaliser des graphes de ces fonctions et à les commenter pour en faire un joli nouveau petit théorème TRM que tu pourras signer de ton nom ! :slight_smile:

14

Correction : x=B/c

En appliquant la formule du post précédent , la formule du temps de doublement du nombre de DU , en partant d’un portefeuille de x DU, est :
1/c (ln(1-cx)-ln(1-2cx))

Merci a Galuel !

15

Dans ce cas on a b = cx, et en remplaçant on aura qu’un individu ayant déjà produit "x = b/c " DU à la date t0 verra sa production doubler au bout de :

t-t0 = 1/c [ln(1-b) - ln(1-2b)] = 1/c ln[(1-b)/(1-2b)]

Sous condition que b < 1/2 [1 - 1/(ev/2)²] pour des individus de durée d’espérance de vie moyenne “ev”, avec c = ln(ev/2)/(ev/2).

16

Ca marche, je suis en tain d’étudier cette fonction et voir en quoi elle peut être utile!

17

Whaouu zetes pas mauvais en math on dirait…

18

J’ai tracé pour c compris entre 5% et 20% la fonction
f(x)=1/c [ln(1-cx)-ln(1-2cx)]

fr.plot.png610×627 3.53 KB

On peut dire que :

  • pour x petit: f(x) # x et f(x)>x, quel que soit c (ça se vérifie avec le développement limité de la fonction)
  • f est croissante donc pour tout x, f(x)>x
  • f(x) tend vers l’infini quand x tend vers 1/2c
  • f(x) n’est pas définie quand x est entre 1/2c et 1/c

On voit donc que le doublement du nombre de DU produits prend de plus en plus de temps jusqu’à devenir très élevé quand x=1/2 1/c (1-1/(ev/2)²) puis simplement impossible.

Pourquoi calculer le temps du doublement? (interprétation):
Un individu dépense seulement les DU qu’il produit. Son portefeuille arrive à 0 au bout d’un temps T0, au cours duquel il a produit x0 DU. Il se demande alors si les DU qu’il va produire à l’avenir vont lui permettre de continuer à vivre de la même façon. Pour celà on calcule le temps T1 nécessaire au doublement , pour le comparer à la première période T0.

Les courbes montrent que T croît avec x, donc T1>T0. Petit à petit, il doit donc se serrer la ceinture.

(1) Pour x petit (initialisation du portefeuille) : f(x)#x, donc T1#x0#T0 (car le nombre de DU cumulés est proche du nombre d’unités de temps pour les produire). On a donc T1#T0.

(2) Plus x augmente, plus le T nécessaire au doublement croît fortement et l’égalité (1) n’est plus vérifiée.

(3) Pour x>1/2c, il n’est plus défini : il ne pourra plus jamais vivre comme au début, avec seulement ses DU. Il devra donc travailler, échanger des valeurs qu’il produit avec les autres membres de la communauté…

Mais je ne vois pas de théorème à l’horizon!

Peut-être un résultat approximatif quand même : on ne peut pas vivre seulement de ses DU. Sachant que dans la TRM, on ne peut pas définir ce qui est nécessaire à la vie!

19

Puis ensuite :

Il me semble qu’il y a une erreur de raisonnement.

En effet si un individu est à 0, qu’il ait ou non produit x0 DU préalablement, le temps nécessaire pour produire x0 nouveaux DU sera le même, et ne dépend absolument pas de ce qui s’est passé préalablement.

L’hypothèse et le raisonnement me semblent donc à revoir :slight_smile:

20

Ayant bien retenu l’histoire de Galilée, quand on a du mal à comprendre ou à modéliser quelquechose, il faut penser à…changer de référentiel! Je passe donc au référentiel quantitatif, et je cherche à répondre à la question suivante :
A quoi correspondrait, dans le référentiel quantitatif, une multiplication par 2 du nombre total x des DU déjà produits ?

Il faut donc calculer le coefficient K tel que : Q(t+T-to)=K.Q(t-to)
où T est le temps tel que x(t-to+T)=2x(t-to) , x en relatif.

Pour mémoire :
T=1/c ln[(1-cx)/(1-2cx)]
x(t-to)=1/c [1-exp(-c(t-to))] , ou encore [1-exp(-c(t-to))]=c.x(t-to)

D’après le §5 de la TRM, en quantitatif, la somme des unités monétaires produites entre to et t est : Q(t-to)=(M/N)(to) exp(ct) [1-exp(-c(t-to))]

Donc Q(t-to)=(M/N)(to) exp(ct).c.x(t-to)
Et Q(t-to+T)=(M/N)(to) exp(c(t+T)).c.x(t-to+T)

Or x(t-to+T)=2x(t-to), et exp(c(t+T))=exp(ct).exp(cT)
On a donc
Q(t-to+T)=(M/N)(to) exp(ct).exp(cT).c.2.x(t-to)=2.exp(cT).Q(t-to)

Donc :
K=2.exp(cT)
Soit K=2.[(1-cx)/(1-2cx)]

En remplaçant le doublement par une multiplication par 1, et donc les 2 par des 1, on trouve K=1, donc ça me paraît bon !

Je propose donc une règle de conversion du relatif au quantitatif.

Voici ce que serait mon théorème :blush: :
A condition d’avoir x<(1/2c), le doublement du nombre x d’unités relatives co-produites par un individu équivaut à la multiplication de la somme des unités monétaires co-produites par un facteur égal à : 2.[(1-cx)/(1-2cx)].

On peut remplacer le facteur “2” par un autre nombre (en remplaçant tous les 2), pour généraliser.

Resterait à trouver la relation inverse (du quantitatif au relatif), et étudier les propriétés de ces fonctions.

21

Je n’arrive pas à comprendre ce qui est du référentiel quantitatif ni ce qui est du référentiel relatif, ni à comprendre exactement quelle est l’hypothèse. Mais plus encore je crois que pour faire théorème il faut trouver un résultat remarquable qui ait une forme - relativement - simple ou élégante (ex pythagore est élégant : c² = a² + b², des longueurs aux surfaces).

J’étudierais aussi des formes simples, comme : quand il se passe ceci en quantitatif, que se passe-t-il en relatif ? Peut-on trouver en étudiant ce résultat général un résultat qui soit “élégant” !?

Ce qui est certain c’est que ce qui est addition en quantitatif n’est pas addition en relatif. Changer de référentiel n’implique pas forcément appliquer les mêmes formules aux termes transformés, autrement dit seules des classes de référentiels particulières conservent les lois (ex en physique : les référentiel inertiels conservent les lois d’addition des vitesses, tandis que les réféfentiels accélérés non).

22

J’ai trouvé un résultat pour un individu pseudo-autonome, à partir des équations :
Q(t-to)=(M/N)(to) [exp(ct)-exp(cto)]
R(t-to)=1/c [1-exp(-c(t-to))]

donc :
dQ/dt = DU(t) = c (M/N)(to) exp(ct)
dR/dt = exp(cto) exp(-ct)

soit :
(dQ/dt)(dR/dt) = constante = DU(to)

23

J’ai mieux compris l’idée :

On voit que plus x augmente et se rapproche de 1/2c, plus le temps pour doubler la production est long, jusqu’à tendre vers l’infini. Or les individus étant mortels, il y a une limite physique pour x.

Je veux donc calculer le nombre maximal d’unités relatives x (correspondant à un temps t1), pour lequel l’individu pourra voir sa production doubler, compte tenu de son espérance de vie.
Ce nombre x est donc maximal dans l’hypothèse d’un individu entré dans la monnaie à sa naissance, et sa production aura doublé pile au moment où il meurt.

On a donc
(t1-to) + 1/c ln[(1-cx)/(1-2cx)] = ev

avec :
x(t1-to)=1/c [1-exp(-c(t1-to))]
Soit : (t1-to) = -1/c ln (1-cx)

D’où :
-1/c ln (1-cx) + 1/c ln[(1-cx)/(1-2cx)] = ev
-1/c ln (1-2cx) = ev

Soit :

x = (1/2c) [1-exp(-c.ev)]

Et avec x = (1/c) (1-exp(-c(t-to)]
Cela donne aussi le temps correspondant (je n’ai pas mis les calculs intermédiaires) :
t1-to = 1/c ln[1-1/2 (1-exp(-c.ev)]

Compte tenu de l’espérance de vie humaine “ev”, le doublement des unités relatives produites n’est pas possible après t1 tel que
t1-to = - 1/c ln[1-1/2 (1-exp(-c.ev))]
t1-to = - 1/c ln[1 - 1/2 (1-1/(ev/2)²) ] avec c = ln(ev/2)/(ev/2)

De même, le doublement des unités relatives produites n’est pas possible au-delà d’un nombre d’unités déjà produites de :
x = 1/2 1/c [1-exp(-c.ev)]
x = 1/2 1/c [1 - 1/(ev/2)²] avec c = ln(ev/2)/(ev/2)

A suivre …

[/quote]

24

Ca me semble juste. Toutefois en tant que physicien je reste un peu sur l’expectative. Parce que intuitivement je sais que t1-t0 est proche de ev/2, ce qu’on ne voit pas dans des formules mathématiques directement (même si en tant que mathématicien je peux retrouver ce résultat par approximations).

Il manque ce qu’il est nécessaire de faire dans toute application dans le monde physique (et l’économie n’y échappe pas), c’est ce qu’on appelle l’application numérique

A.N. : pour ev = 80 ans et c = 10%/an on obtient … (on remplace les variables et constantes par leurs valeurs dans les formules, puis on donne les résultats obtenus).

25

Dear Sofrani, dear Galuel,
is it possible to quickly summarize the essence of your conversation in english? I believe, as far as my little french is telling me, that there is some valuable input, which might be interesting for other people and me.

26

It is only mathematical development of the Relative Theory of Money, that is now fully translated into english and published in this URL. you have also other works in english in this URL.

You could publish a site referencing those works in english and publish your own.

27

Thank you Galuel!

28

Just to warn you, this is a first raw translation. A better text has to be released in the next month following the first fixes brought to the text !

So you can find mistakes but you can already start to read it :wink:

2 Likes
29

@Sofrani, could you be so kind and try to explain me your calculations in english? I really would like to understand!

30

Application numérique :
Pour ev=80 ans et c=10% : t1-to=6,9 ans soit 17% de 40 ans (ev/2)
Pour ev=40 ans et c=10% : t1-to=6,7 ans soit 34% de 20 ans (ev/2)

(t1-to) peut ainsi ne pas sembler très sensible à ev à première vue (6,9 contre 6,7 ans)…mais il faut aussi réflechir par rapport à la valeur de ev/2.

Par analogie avec d’autres phénomènes physiques, j’appelle « demi-vie » ce temps. La « demi-vie » est le temps mis par un individu pour produire la moitié de ce qu’il aura produit en DU au total sur ev, dans le référentiel relatif.

Je divise donc ma formule par ev/2 pour pouvoir mieux étudier cette « demi vie » exprimée en proportion de ev/2.

(t1-to)/(ev/2) = - [1/ c.ev/2] ln[1-1/2 (1-exp(-c.ev))]

On voit que c’est une fonction de la variable « c.ev », dont voici ci-dessous le graphique.
Pour 80 ans et 10%, on est à c.ev=8, et on retrouve 0,17.

La demi-vie est égale à ev/2 seulement pour c.ev=0.

Je définis la « demi-vie » comme le temps mis par un individu pour produire la moitié de ce qu’il aura produit en DU au total sur ev, dans le référentiel relatif. Pour l’ensemble des monnaies libres et quelle que soit ev, il existe une fonction unique et bijective qui relie le rapport « demi-vie/(ev/2) » d’une part, et le produit « c.ev » d’autre part.

A venir : une interprétation graphique, un peu à la manière du « rectangle d’or ».

DemiVie.png1123×794 27.9 KB

31

@Samuel I’ll make translations if it’s worth it! (not sure for the moment)

32

C’est pas mal, mais le terme percute 1/2 ev. Je te propose de l’appeler plutôt : “temps de 1/2 production”.