Je ne participe pas de suffisamment près à ce que vous faite pour venir donner un avis éclairé, mais je trouve le travail que vous être entrain de faire génial ! Bravo à vous ! 
Est ce qu’on ne pourrait pas tout simplement compter, pour un membre m, le nombre de membres dont m est à une distance inférieure ou égale à maxStep dans le sens certifié → certificateur ?
Ou encore plus simplement, le nombre de membres dont la distance à m est inférieure ou égale à stepMax dans le sens certificateur -> certifié, ce qui est équivalent.
Ou, peut-être encore plus significatif, le nombre de chemins les plus courts joignant m à tous les membres dont la distance est inférieure ou égale à maxStep dans le sens certificateur -> certifié. Chaque chemin dénote une influence dans la règle de distance.
Ça reviens a calculer la distance en considérant que tout le monde est référent, on perd tout l’intérêt de la notion de centralité ![]()
Même remarque qu’au dessus.
Cela est déjà plus proche de la notion de centralité, on peut essayer ça ![]()
Dans le dernier cas, on ne tient pas compte des référents non plus. Je ne vois pas bien la différence. Dans les autres cas, cela voudrait dire qu’on ne fait le calcul pour m que si m est référent ? Pas de calcul pour les autres membres ?
J’ai écrit l’algorithme pour le dernier cas :
Distance Stress Centrality.pdf (304,7 Ko)
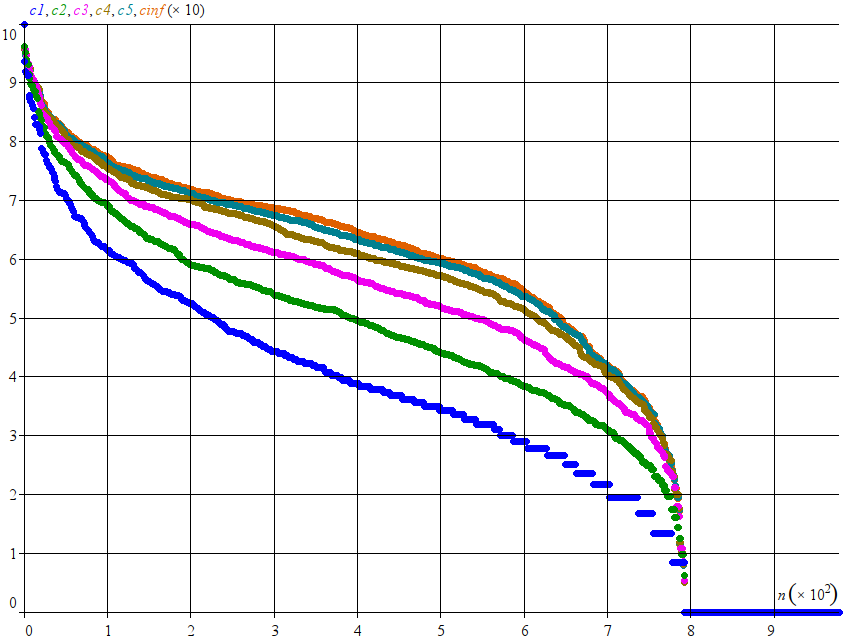
Cela donne ceci pour différentes valeurs de maxStep (1, 2, 3, 4, 5 et infini) :
Tu remarqueras qu’il y a peu de différence entre les courbes gris-bleue (stepMax = 5) et orange (stepMax infini). L’ordre des membres est peu modifié aussi.
Temps de calcul, en ms :
c1 : 102
c2 : 197
c3 : 461
c4 : 612
c5 : 695
cinf : 716
Ah, j’ai oublié de préciser que dans le dernier algorithme, la relation v -> w est dans le sens certificateur -> certifié obligatoirement. Le calcul n’est plus symétrique, sauf pour cinf, bien sûr.
Merci beaucoup je vais regarder ça et l’implémenter dés que je peut ![]()
C’est normal la wot du bloc zéro est très petite, je me plonge dans la perspective d’une wot mature a qq millions de membres, la différence sera alors importante !
Arf passer de 40ms a 695ms ça fait mal niveau perf, peut être que cette valeur sera plus faible en Rust toutefois, on verra bien lorsque j’aurais implémenter ça !
Oui j’y est pensé, je vais devoir jouer d’une astuce pour avoir les liens dans l’autre sens, j’ai ma petite idée ^^
Il y a quiproquo. J’ai fait les calculs sur la WoT complète. Les temps de calcul ne poseront pas de problème avant un moment.
Trop bien, en voila une bonne nouvelle, je me disais aussi que nous prendre un facteur 15 c’était bizarre !
Évidemment, avec quelques millions de membres, le temps de calcul sera plus long. Il varie selon O(n.m) où n est le nombre de membres et m est le nombres de liens, qui lui même, si la densité des liens ne change pas, est proportionnelle à n ². Donc, pour, mettons, 1 million de membres, le temps de calcul serait de l’ordre de (10^6 / 10^3)^3 * 0,7 = la bagatelle de 700 millions de secondes ! Heureusement que c’est l’algo le plus rapide que nous ayons pour l’instant  .
.
Je pense qu’a long terme il nous faudra concevoir des algorithmes qui estiment une valeur proche de la grandeur voulue en parcourant un grand nombre de chemins aléatoires afin de conserver un temps de calcul exploitable !
Je me suis trompé. Heureusement. m est bien proportionnel à n ², mais le dernier algorithme limite le calcul à 5 pas, donc on peut considérer m comme constant. Du coup le temps de calcul est proportionnel à n. Pour 1 million de membres, il ne fait plus que 700 s, ce qui est tout à fait gérable  .
.
Et encore même pas, puisque chaque membre est limité a 100 certifs, et tout le monde ne s’en servira pas, dans une toile mature on devrait tendre au maximum vers m = 70n.
En fait, les deux limitations sont importantes. Le nombre limité de certifications par membre limite en largeur le réseau traité par l’algorithme à partir d’un membre donné, et la constante maxStep le limite en profondeur. Au final il y a une limite supérieure constante au nombre de nœuds traités par l’algorithme par membre (sigStock^maxStep - 1 = 100^5 - 1). C’est gros mais on sera en moyenne très en dessous.