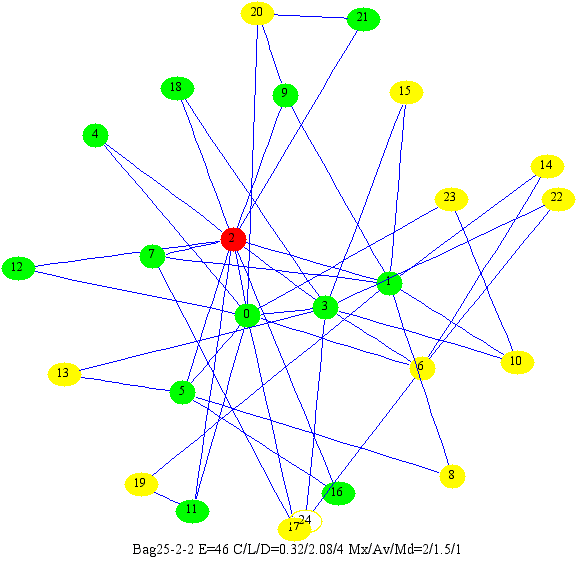
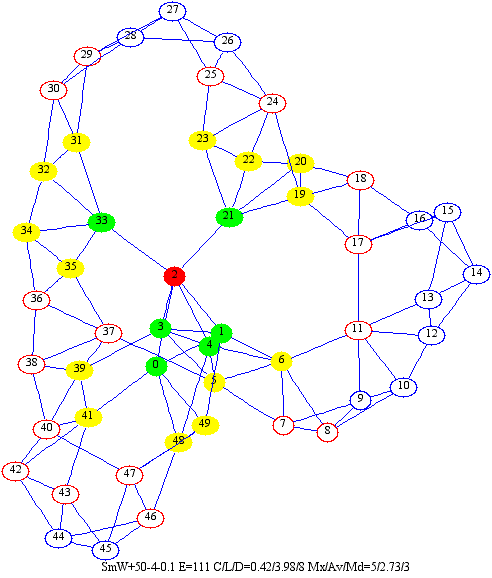
Bonjour,
Dans le cadre de l’analyse des WoT, le nombre de liens et de noeuds rendent la chose complexe. Il faudrait utiliser des métriques pour pouvoir mesurer et analyser ces WoT. Ici, je vais d’abord expliquer quelle forme vont prendre les WoT selon moi. Je vous laisserai ensuite compléter ce topic avec vos analyses et métriques envisagées.
Modéliser une WoT Duniter
Pour ce faire, je vois au moins 2 typologies de WoT aléatoires à utiliser :
Scale free Networks
-
Via le modèle de Barabási–Albert via le générateur : barabasi_albert_graph — NetworkX 1.7 documentation
Cet algorithme utilise une notion de préférence : les nœuds ayant déja des liens sont plus susceptibles que les autres d’en recevoir à nouveau. “Rich get richer”. Ces graphs n’ont pas de limite de taille. A mon avis, ce n’est pas le meilleur modèle pour une WoT.
-
L’algorithme de Holme et Kim via le générateur : powerlaw_cluster_graph — NetworkX 1.7 documentation
Cet algorithme utilise une notion de préférence : les nœuds ayant déja des liens sont plus susceptibles que les autres d’en recevoir à nouveau. “Rich get richer”. Cependant, ce modèle a tendance à former des clusters contrairement au modèle BA. -
La distribution des « certifications » (degree distribution) suit une courbe « power law ».
Cela semble incompatible avec les règles actuelles de Duniter qui fournit un stock de signatures identique pour tout le monde.

Small World Networks
- Via le modèle de Watts et Strogatz via le générateur : newman_watts_strogatz_graph — NetworkX 1.7 documentation
Cet algorithme génère des graphs avec des propriétés de Small world. Ces propriétés sont intéressantes dans le cadre d’un WoT : la plupart des noeuds ne sont pas voisin des autres, mais la plupart peut être atteignable depuis n’importe quel autre noeud en un nombre faible de rebonds.
La « degree distribution » de ce modèle suit une courbe de Poisson :
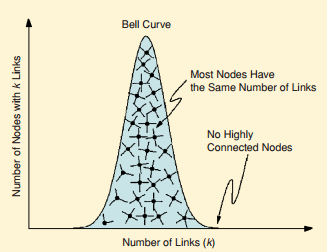
Il semble que la plupart des Small World Networks de la vie réelle sont de type « Scale Free ».
Néanmoins, on peut imaginer influencer le comportement des utilisateurs d’une toile de confiance Duniter en suggérant des certifications. et ainsi créer une topologie de graph qui nous arrange.
Après avoir lu sur les Small World Networks, je dirais que les WoT Duniter s’en rapproche à plusieurs titre :
Small-world properties can arise naturally in social networks and other real-world systems via the process of dual-phase evolution.
This is particularly common where time or spatial constraints limit the
addition of connections between vertices The mechanism generally
involves periodic shifts between phases, with connections being added
during a “global” phase and being reinforced or removed during a “local”
phase.
On a de la chance, il semble que ce type de toile est naturellement plus robuste :
It is hypothesized by some researchers such as Barabási
that the prevalence of small world networks in biological systems may
reflect an evolutionary advantage of such an architecture. One
possibility is that small-world networks are more robust to
perturbations than other network architectures. If this were the case,
it would provide an advantage to biological systems that are subject to
damage by mutation or viral infection.
Hypothèse : une WoT duniter est modélisé par un small wot network
Hypothèse à faire valider par des simulations, analyses expérimentales.