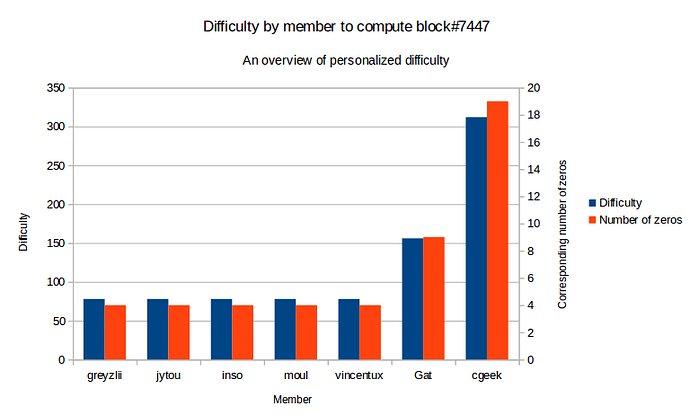
Also, this is a good moment to show you the associated difficulty graph:
Here are some keys to decode this graph:
- blue columns give the raw difficulty
- red columns give the equivalent number of required zeros for the proof-of-work
- the common difficulty is
78 - this common difficulty of
78is equivalent to4zeros
How is decided common difficulty? It is computed accordingly to the speed given by the number of blocks computed by a period of time. If the speed is too high, common difficulty increases, if too low, it decreases, otherwise it do not change.
This is a mechanism to always have the same speed of calculation for a block, on average.
You can see on this graph that the personalized difficulty of 5 of these members equals to 78: greyzlii, jytou, inso, moul and vincentux.
You can also see that the personalized difficulty of Gat equals to 156, and cgeek equals to 312. This is the rotation mechanism.
Considering this observations, and with the Duniter rules in mind, I can say that:
- the very last block (#7446) was issued by cgeek
- the previous block (#7445) was issued by Gat
- the other members may have issued block #7444 or whatever block before (in the limit of 100 block, so at max block #7347, protocol parameter
blocksRot = 100for TestNet)
Also, I understand that if one of [greyzlii, jytou, inso, moul, vincentux] succeeds to compute block #7447, then Gat will come back to common difficulty 78, cgeek will decrease to difficulty 156, and the succeeding member will have difficulty 312.
This is how rotation works.
DIfficulty.ods (33,9 Ko)