Note
I am going to do this in english first, adding a french version if I get the time. I will probably edit this post in the future. Feel free to ask questions.
Abstract
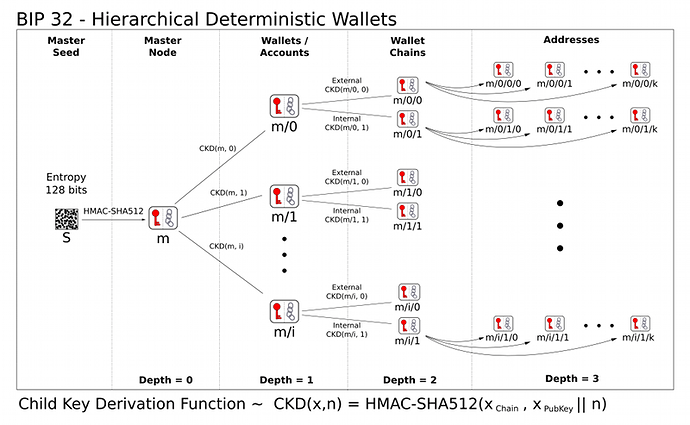
The 32th bitcoin improvement proposal describe a way to derive public/private keys couple (secp256k1) from a 256 bit seed. Futhermore, it allow to organise the keys in a tree forming a wallet with subwallets you should be able to share without compromising the privacy of the others keys of your wallet.
The master key
The way you obtain this is not really important. From a 256bit seed generated from a PRNG, you HMAC-SHA256 this with the key “Bitcoin seed”. The first 32 byte constitute the private key and the second 32 bytes constitute the chaincode.
ChainCode is really important, it’s 256bits entropy that allow you to compute subkeys. This way you can share the public key freely without being afraid that the guy you gave this child private key would be able to know your parent private keys (and then all the descending private keys).
An extended key (k, c) is a key of 256 bits + a chain code of 256 bits. In the rest of this post, I will denote the private keys as k and the public keys as K.
The tree
Fist of all, you should know that bip32 describes two type of keys couples, the hardened ones and the non-hardened ones. First I’ll talk of the non-hardened ones which are specific to bip32 only talking about the non-hardened in the end.
So now you get the extended master keys (k, c) and (K, c) you will derive a child private key of index i by f(K, c, i) + k. This way, the public key will be G.f(K, c, i) + K. You should remark that I only use the extended public key to get the public child key.
f is the 32 first byte of HMAC-SHA256 with the chaincode as a key and the data being K and i. The second 32 bytes constitute the child chain code.
The hardened keys are computed bay the formule f(k, c, i) + k. This way you cannot compute the child public key without knowing the child private key.
Keys notation
Thay note the keys in the tree starting from master m. m/2/5h/3 would be the 3rd non-hardened child the 5th hardened child of the 2nd non-hardened child of the master.
Advantages
You can implicitly store used public keys by indexes range allowing fast and secure audit of the wallet.
You can create secure subwallets from m/*h.
You can share m/ih extended with a trust business to anonymize your transactions (using a different subkey each time : this is really useful)
You can share m/ih extended with an insecure money receiver (webserver) without compromising any othe key in your wallet.
Incovenients (Security)
Knowing an extended public key and a child private key compromise the subwallet (by subtracting f(Kpar, c, i) to kchild).
Index search is easy therefore index should not be considered as a security feature of bip32.
Final Note
This post should help you to read the bip32 which is rather formal but definitly clearer than what I wrote above. Thank you for your attenion !