It’s more 10-11% / mois than 20%.
I have actually done the following calculations based on the graph of the numbers of members in cesium (you can double-check the numbers yourself):
The formula to calculate the percentage is: (current - previous) / previous x 100. Did I mess up something?
Note: I believe that the rate slowed down after a few months because the licence started getting respected more strictly, but that’s just my own intuition.
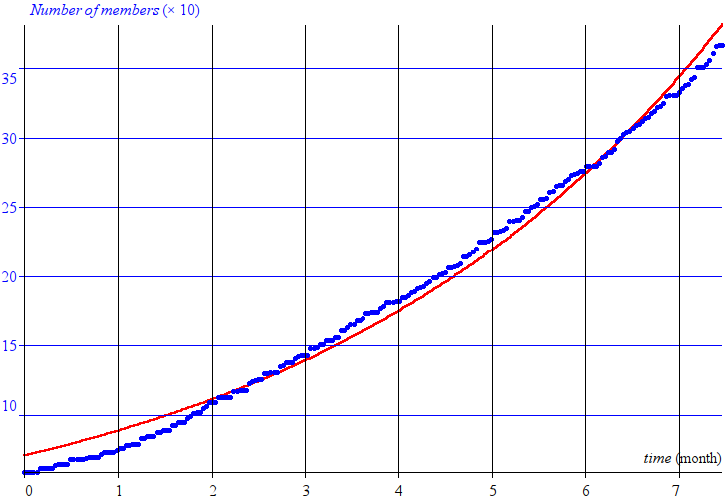
Your calculation is correct if you consider that the growth is evenly exponential, which is not exactly the case.
But if you consider that, during the first month or so, the growth was linear, it gives you a new picture, with a much better fit.
In this case the second part of the curve (after the first month) is an exponential with a rate (today) of 11.4 +/- 0.4 % / month.
Note that this value is a mean over a rather large period. If you calculate over a smaller sample, the result may be quite different.
I’m not sure how you calculated this value of 11.4.
From approximately 28 on your graph in month 6, if we add 3.2 (which is 28 x 11.4%), we get 31 for month 7, not 33 as can be seen in the same graph.
And if we start a series from month 2 (108 members on 08/05 which actually matches your graph) and add 11.4 % every month (with a simple formula where we take the result from the last month and multiply it by 1.114), we get:
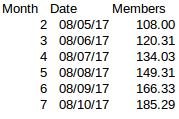
Which is far from the 330 or so on month 7. The same goes with other months.
If we apply a 25% growth rate starting at month 2, however, we do get 330 at month 7:
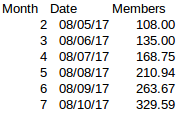
So I am puzzled about how you obtained the “rate of 11.4%”. Could you give the detail of your calculation?
Actually I don’t assume that anything ls linear or exponential. I just observe the growth month after month, compared to the previous month, not “overall”. If by observing that we get a “reasonably stable value”, then the growth is exponential-like on the interval where this “reasonably stable value” is observed. Of course, depending on the day of the month on which you observe, there may be some variations in my very imperfect measurement, but it still gives a general idea of where all this is heading.
I use a nonlinear regression with the following function:
f(t) = if(t < tL, a1 * (t - tL), a2 * (exp(c * (t - tL)) - 1)) + b
i.e., for t < tL, it’s a linear function f(t) = a1 * (t - tL) + b, and, for t >= tL, it’s an exponential function plus a constant value: f(t) = a2 * exp(c * (t - tL)) + b - a2. With these values, the whole function is continuous, in particular at t = tL.
The calculation process tries and finds the values of the parameters tL, a1, a2, b and c that minimize the quadratic distance between the measured values and the function. It leads to a value of 11.4 % / month for c.
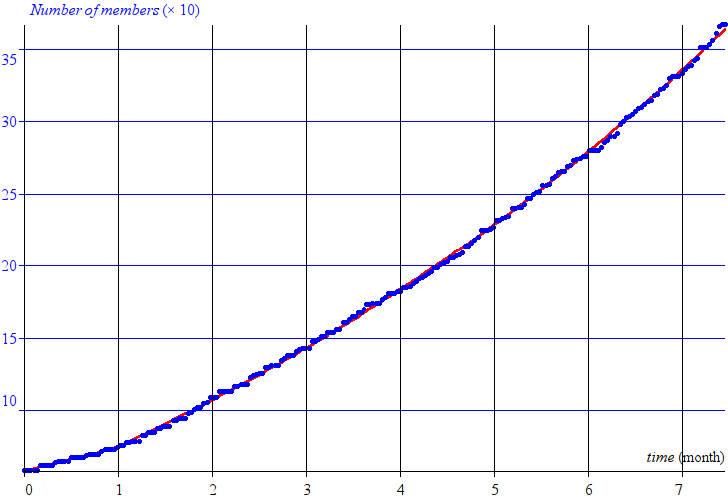
The key point is that the second part of this model is not a simple exponential, but an exponential plus a constant. As you can see above, a simple exponential doesn’t fit the measured values. This is the main reason why our both calculations don’t agree.
@eukreign sorry for the disturbance.
I see, so 11.4 is one of the parameters of this extrapolating function, but it does not reflect the actual monthly growth rate, it is only a parameter of a function (which by the way is inside an exp function). It’s as if you were extrapolating with f(x) = a * sin(b x + c) + d and giving me the value of b.
Anyway, I guess we’ve trolled @eukreign’s post good enough, sorry for that!
To answer the actual questions, I would say that:
- the growth being already quite fast, I don’t consider it an “issue” that “needs to be solved” on this point,
- enabling people outside the WOT to generate UDs causes problems as I have already mentioned in my first answer,
- people are already “placed in a queue” to join the WOT as it is today: either they move around to get closer to existing members, either they wait patiently for the WOT to come to them, which will happen after some time. As for them not accumulating UDs in the meantime, I don’t see it as a real problem. After all, if they did produce UDs now, these UDs would lose some value until they finally enter the WOT (along with causing problems on the monetary mass as I have already pointed out), and on the long term these UDs would simply be worth peanuts.
Besides, the introduction of a central database in a fully decentralized system is kind of a paradox and could lead to serious problems (security, centralized authority and its drawbacks, etc). We generally want to do the opposite. It seems to me that the real solution to the problems of “exclusion” is “patience”, which solves pretty much all the problem without introducing new ones.
So even if we wished to, I don’t think there is any way of implementing this, not in the current version of duniter, and probably not in the near future, but I’ll let the devs comment on it if they have further ideas.
Of course, anyone can start their own currency with different rules (for instance certify upon seeing someone’s ID in random video meetups or whatever means) and see how it goes. I bet this would collapse quite quickly but of course I might be wrong. The WOT as it is today is a result of years of thinking…
Just say : M1(2017/10/22) = f(t) = if(t < tL, a1 * (t - tL), a2 * (exp(c * (t - tL)) - 1)) + b
And just wait until t2 = 2019 / 2020 what happens to this model in front of experimental measures, and then :
- (1) If it’s still ok, just keep it
- (2) If it’s not ok, just find M2(t2)
- (3) Go back to (1)
Any place other than cesium where one could view this data?
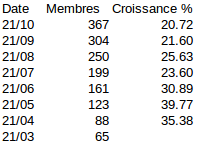
Date Members Growth
2017/03/21 65 NA
2017/04/21 88 35.88
2017/05/21 123 39.77
2017/06/21 161 30.89
2017/07/21 199 23.60
2017/08/21 250 25.63
2017/09/21 304 21.60
2017/10/21 367 20.72
2017/11/21 448 22.07
I’ve written a little piece of code that calculates the size of the WOT day by day. It’s a by-product of WotWizard, that I never planned to publish.