Attention j’ai l’impression que tu mélanges les choses, tu ne peux pas faire un pourcentage d’une soustraction.
Là tu dis que le DU a pris 42 centimes en 4,5 ans ce qui fait 9,33 centimes par an et non 9,33 %.
Attention j’ai l’impression que tu mélanges les choses, tu ne peux pas faire un pourcentage d’une soustraction.
Là tu dis que le DU a pris 42 centimes en 4,5 ans ce qui fait 9,33 centimes par an et non 9,33 %.
Pour moi, pour calculer un taux de croissance, il faut calculer un différentiel sur un différenciel fois cent :
c = {ΔDU \over Δt} × 100
Le DU a été réévaluée de 0,933 Ğ1 en moyenne par an, soit :
DU(sept 2021) = 10,00 Ğ1 + 0,933 Ğ1 × 4,5 ans ≃ 10,42 Ğ1
Pourquoi penses-tu ça ne soit pas un calcul correct pour calculer le taux de croissance ?
Ton c devrait être un pourcentage donc un nombre sans unité alors que là c’est des junes par an.
Si je suis ton raisonnement, j’ai un c qui vaut 2% la première année, 5% la 2eme, 9% la 3eme, 16% la 4eme, 20% la 5eme. Effectivement ça fait à peu près 10% sur 4-5 ans mais je ne suis pas sur qu’on retrouvera ce résultat par la suite.
L’endroit où je me suis trompé dans mon raisonnement, c’est que le taux de croissance c concerne la masse monétaire, par le DU. Dans ma démonstration je l’ai appliqué au DU, et comme tu le fais remarquer le résultat colle pour 4,5 années, mais ça devient absurde pour d’autres valeurs. Merci pour ça.
Je n’ai pas encore réussi à calculer correctement le taux de croissance c pour la masse monétaire M. C’est ça qui nous intéresse…à nos calculettes 
Tant qu’on y est, pourquoi c’est forcément soit t soit t-1 ?
Pour approcher les solutions d’équations différentielles on peut aussi utiliser t-\frac{1}{2} (le point milieu) ou \frac{1}{2}((M/N)_t+(M/N)_{t-1}) (la moyenne) par exemple.
J’ai testé plusieurs méthodes, la plus précise est celle avec (M/N)_t. (je mesure la précision à la distance aux résultats obtenus quand la période de réévaluation est très petite. Toutes les méthodes convergent quand cette période est assez petite.)
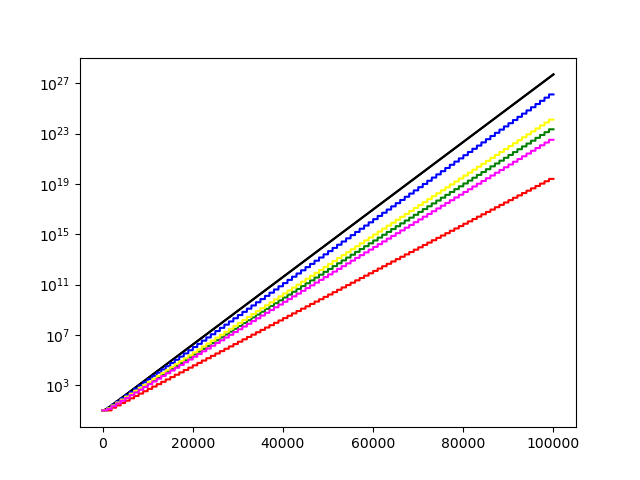
(x=temps, y=DU) Sur cette simulation, N a une croissance exponentielle.
Il faut encore vérifier si certains choix dans la simulation influencent les résultats, notamment l’ordre dans lequel les opérations sont faites, et la croissance de N.
Un pourcentage est un produit en croix, si tu multiplies par 100, il faut que tu choisisses l’équivalent du 100 dans ton unité qui servira de diviseur. Par exemple on peut prendre DU(0) comme diviseur pour étudier la croissance du DU durant ces 5 dernières années : ((10,52 - 10) / 10) x 100 = 5,2% pour 5 ans.
Cette croissance sera de 10% par an quand M/N = 1/c pour que c² x M/N = c² x 1/c = c. Elle est de 1-2% actuellement, car la monnaie est dans sa phase de création et le nombre de junistes croît d’année en année. D’après mon simulateur (à prendre avec des pincettes, je suis pas tout à fait sûr de mes résultats  ), avec la formule actuelle du DU et un nombre de junistes qui croît de façon linéaire de 750 personnes par an (ce qui correspond à peu près à ce qui a été observé jusque-là dans la june) on attendra les 10% de croissance dans 100 ans (et de 9% dans 40 ans).
), avec la formule actuelle du DU et un nombre de junistes qui croît de façon linéaire de 750 personnes par an (ce qui correspond à peu près à ce qui a été observé jusque-là dans la june) on attendra les 10% de croissance dans 100 ans (et de 9% dans 40 ans).
Je pense que la réponse de tuxmain devrait clore le débat.
Il faudrait d’ailleurs compléter la page Duniter | Monnaie libre avec la formule de discrétisation utilisée pour Duniter parce que pour l’instant je me suis permis d’y mettre ma formule continue (avec un c différent)
\mathrm{DU} = c\frac{M}{N}\mathrm{d}t
Oui, merci, c’est bien la formule suivante pour calculer un pourcentage qui n’a pas de dimension.
c(DU 5 ans) = {{10,52- 10,10} \over 10,00} × 100 = 5,2 \%
Bien vu, la croissance de la masse monétaire Ğ1 (M) ne sera stabilisée lorsque le nombre de membres (N) le sera. Du coup, ça me semble sans intérêt de corriger la formule de réévaluation du DU pour Substrate.
5,2% en 5 ans, c’est loin des 4.88 % tous les six mois. On le sait tant qu’on n’est pas en monnaie pleine cette croissance sera très faible.
La formule pour avoir en monnaie pleine une croissance de 4.88% par semestre est celle indiqué par Galuel dans le deuxième message de ce post. Formule du DU - #2 par Galuel
Mon calcul ne concerne pas le taux de croissance de M mais celui du montant du DU.
Ce point rejoint ma critique sur ce qui est affiché dans Cesium :
On ne donne pas d’information pertinente quand on change d’unité de mesure (croissance en jour, alors que la croissance cible est exprimée sur 6 mois).
Il ne faut pas confondre :
Il convient donc de calculer la croissance monétaire sur 6 mois pour la comparer avec le taux de croissance cible.
Le graphe sur la monnaie devrait être légendé “masse monétaire moyenne M/N” et pas “masse monétaire”.
Parler de la masse monétaire Ğ1 n’est pas pertinent sans la rapporter au nombre de membres, et le graphe gagnerait ainsi en clarté si la courbe jaune représentait le taux de la croissance effective de la masse monétaire moyenne (en %).
Question : comment a évolué de 6 mois en 6 mois le taux de la croissance effective de la masse monétaire moyenne ?
En période de mise en place, tant qu’on n’est pas en monnaie pleine (une moyenne de 3800 DU par membre et un nombre de membres stable) le taux de variation de M ou même de M/N ne sont pas significatif (ils sont tellement énormes). Bien que le dernier taux de croissance de M/N soit un peu plus raisonnable (6,65% à comparer au 687.94% entre mars et septembre 2017)
Il me semble plus important de se focaliser sur ce que ça donne en monnaie pleine.
Pour avoir une croissance de c par semestre la bonne formule du DU quotidien recalculé tous les 6 mois est : DU(t+1) = DU(t) + c² (M(t)/N(t))/182.625
Ils sont significatifs si on regarde leur variation. Cela permet de comprendre comment on passe de la création à partir de “rien” (au sens de l’objet inexistant, pas du tout inexistant) à la création à partir de quelque chose.
Avec une échelle logarithmique ça devient raisonnable. Une exponentielle devient linéaire, et on peut étudier la pente facilement.
Taratata ! En mathématiques il ne s’agit jamais de déclarer “pour moi”, “je pense que”, “j’affirme”, et toutes ces genres de choses. Le mieux étant donc de procéder par étapes simples pour aboutir à un résultat.
Première étape : peux tu écrire la formulation de base qui lie le DU à M/N ?
Cette formule est importante, je te laisse donc t’en occuper.
Je suis dans une phase d’observation sur ce sujet. On verra si je continue à développer pour la June suivant la direction que prendra ce sujet et celui sur substrate.
Observe donc :
(a) DU(t) = c.(M/N)(t) est vrai aussi à t+1 :
(b) DU(t+1) = c.(M/N)(t+1)
(b) - (a) = DU(t+1) - DU(t) = c.[(M/N)(t+1) - (M/N)(t)]
Or par définition : (M/N)(t+1) = (M/N)(t) + DU(t)
D’où : DU(t+1) - DU(t) = c.DU(t)
En remplaçant DU(t) selon a) on obtient donc :
DU(t+1) - DU(t) = c².(M/N)(t)
Et donc in fine : DU(t+1) = DU(t) + c².(M/N)(t) CQFD
Note : ce calcul est démontré depuis 2016 sur cette page.
Je ne remet pas en question la justesse mathématique, je veux juste la traduire en pseudo code pour ma compréhension personnelle, et donc aussi pour la coder si besoin dans un client.
En mettant ta démonstration dans un tableur, je pense que mon incompréhension vient de ce que l’on entend par « t ». Avec en définitive (à me confirmer) :
t+1 : le futur
t : l’instant présent (du calcul dans notre cas)
t-1: l’instant du calcul du DU précédent
J’'avais l’impression (erronée) que pour certains, t était t-1…
Tu peux très bien choisir ces définitions pour “t” oui, “t” vaut n’importe quel moment.
Mais je ne suis pas sûr que ça t’aidera, car tu devras bien calculer DU(t) pour justement aller “dans le futur” selon : DU(t) = DU(t-1) + c².(M/N)(t-1)
Et donc oui le calcul dépend du (M/N) “passé”, et du DU “passé” qui donne une information sur le “présent”, puisque (M/N)(t) = (M/N)(t-1) + DU(t-1).
Il faut voir le DU(t-1) comme le bout de droite qui relie (M/N)(t-1) et (M/N)(t) en imaginant que chaque (M/N)(t) est un point discret qui forme une fonction discrète généralement croissante (croissante pour N stable notamment).
Le mieux pour comprendre est de poser DU(0) = 100, et (M/N)(0) = 0 dans un tableur, et de constater que ça converge de manière très fluide et très limpide.
Un message a été scindé en un nouveau sujet : Production du DU