Apparemment il y a un soucis avec la formule actuelle du DU dans Duniter.
La formule correcte est DU(t+1) = DU(t) + c² (M/N)(t)
Mais changer les indices en « t » ou « t+1 » n’est pas significatif, c’est juste théoriquement un peu moins « propre ».
peut etre c4 au rythme des saisons temperées ? non c bien comme ça
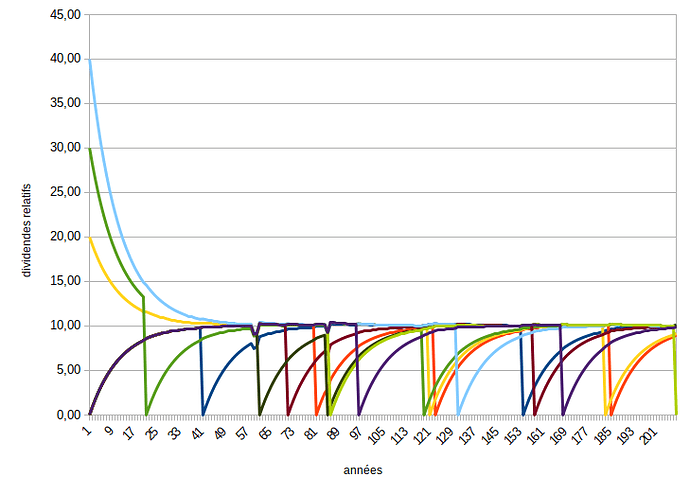
j’ en profite pour partager ce graph avec différentes longévités 2o-13o ans, les variables sont modifiables en quelques clics
evvariant.ods (153,7 Ko)
obtenu sans bagage informatique ou mathématique grace à cette capsule
Moi aussi je préfère la formule
DU(t+1) = DU(t) + c² (M/N)(t)
Parce qu’elle permet de connaitre précisément à l’avance le DU futur. Si on veut faire des billets libellés en DUğ1 par exemple.
Si je comprend bien, le bug n’est pas la formule mais les arrondis des nombres flottants qui ne sont pas déterministes. (@cgeek tu confirmes ? Si oui il faut renommer le sujet en « bug nombres flottants dans la formule du DU »)
Pour la formule à utiliser (on en a déjà discuté longtemps sur tous les fils cités), celle qui a été actée est :
DU(t+1) = DU(t) + c² (M/N)(t+1)
Pour la simple raison que lors du calcul, il faut prendre N courant et pas N d’il y a six mois si on veut respecter la symétrie spatiale au moment du calcul.
Si vous voulez relancer le débat, je pense que le mieux est de créer un autre sujet et de déplacer les messages dedans.
J’ai un doute sur ces deux affirmations.
Pour la première, c’est le sujet du lien du post, Elois après discussion avait acté cette formule pour son implémentation :
Pour la seconde, quand tu calcules le DU, tu es d’accord pour dire que le N réel est le nombre de membres au moment du calcul ?
J’ai interprété tes affirmations différemment ce matin. Après relecture et réflexion, ces deux affirmations me semblent corrects.
Si si, c’était bien le problème originel, qui prend sa source ici.
D’ailleurs je n’arrive pas bien à discerner si j’avais vraiment faire une erreur à l’époque ou non, vu que c’était Galuel qui avait fait un commentaire que j’ai saisi en ticket et m’avait fait changé le M(t) en M(t+1) (ou l’inverse, je n’arrive plus à savoir).
edit : le ticket en question.
D’où le présent sujet.
En utilisant des exemples, je trouve que la formule DU(t)=c * M(t)/N(t) est équivalente à DU(t+1)=DU(t)+c^2 * M(t)/N(t), et n’est pas équivalente à DU(t+1)=DU(t)+c^2 * M(t+1)/N(t+1), le tout avec N stable.
Mais on peut aussi imaginer une formule DU(t)=c’ * M(t-1)/N(t-1), avec un c’ légèrement différent de c, qui soit équivalent à DU(t)=c * M(t) /N(t). Pareil pour l’autre forme de formule.
Du coup je pense que les deux formules sont possibles, ainsi que leurs intermédiaires (t=t+0,5… :p)
C’est bien l’inverse, @Galuel m’avait fait changer M(t+1) en M(t) via sa remarque que j’avais saisie dans le ticket #878.
Eloïs a décidé de faire machine arrière sur ce changement dans cette discussion du forum ML.
Quant au N(t+1), ça a toujours été cette implémentation. C’est le juste M qui était pris en +1, puis +0, puis qui reviendrait en +1 avec Duniter V2S.
Merci, j’avais un doute puisque le débat semblait clos. Comme il est relancé et qu’il est critique pour moi car il détermine la symétrie spatiale, je vais essayer de préciser mon point de vue.
J’essaie de convertir la phrase compréhensible par la plupart des gens non matheux et qui m’a amenée sur le projet :
Lors de la création monétaire annuelle, on augmente la masse monétaire de 10%, somme que l’on répartit à parts égale à tous les membres. Le montant de cette part est appelé Dividende Universel.
Pour moi cela correspond à :
DU(t+1) = DU(t) + c² (M/N)(t+1)
Si je convertit l’autre formule, qui prend M et N à t (6 mois avant dans Duniter, mais 1 an avant dans les exemples annuels), j’obtiens :
Lors de la création monétaire annuelle, on augmente la masse monétaire d’il y a un an de 10%, somme que l’on répartit à parts égale à tous les membres, sur le nombre de membres qu’il y avait il y a un an. Le montant de cette part est appelé Dividende Universel.
Le DU n’étant pas calculé pour le nombre de membres existants lors de ce calcul, je ne vois pas comment on peut respecter la symétrie spatiale.
Là est mon problème avec l’autre formule.
Je ne pense pas que ce soit ça ton problème, car la symétrie spatiale c’est “tout membre de la WoT co-crée la même part de monnaie en même temps”, ce qui est tout le temps vrai dans Duniter peu importe la formule.
Du coup, je partirais plus sur la formule suivante pour plus d’exactitude :
- DU(t) = DU(t-1) + c² (M/N)(t)
Ça change rien à ce qui sera implémenté dans Duniter. C’est pour que ce dont on parle soit plus précis mathématiquement. C’est exactement la même formule, mais avec un décalage du temps.
Elle signifie le calcul du nouveau montant du DU au moment de la réévaluation (à t) est basée sur la valeur du DU de la précédente réévaluation et M et N au moment de la réévaluation actuelle (t).
Merci cgeek et Moul, c’est exactement ça mon problème : le décalage dans le temps du calcul, qui l’éloigne de la réalité.
La symétrie spatiale n’est pas impactée, c’est vrai.
OK mais de toute façon il y a des variations entre t et t+1, quelque soit la formule, et je n’ai pas l’impression qu’il y ai de différence sensible sur la symétrie temporelle, Galuel non plus, je crois lire que @yyy ci-dessus non plus.
Côté technique Eloïs arguait que c’était plus simple avec M(t+1), honnêtement cette simplification est dans l’épaisseur du trait selon moi.
Oui, de ce que je me souviens de cette discussion, c’est que ça ne change pas grand-chose d’un point de vue symétrie temporelle à l’échelle actuelle de développement de la Ğ1 (~ 4 000 membres) Le montant du DU va légèrement être au-dessus ou en dessous de la valeur théorique souhaitée, mais de toute manière la TRM n’est pas précise concernant de taux de croissance c. Si avec la formule actuellement implémentée dans Duniter ça met en place un taux de croissance entre 9 et 11 % par an, ça ne devrait pas faire grande différence dans l’économie actuelle. C’est une variable que les générations futures pourront s’amuser à faire varier pour étudier l’impact de ce taux de croissance sur l’économie au cours de plusieurs générations.
Pour ma part, ce changement peut être planifié pour après la migration sur Substrate, pour ne pas surcharger la transition déjà conséquente.
Je sais pas trop
Avec N constant M/N à t+1 est supérieur à M/N à t.
Si on choisit l’un ou l’autre on a une augmentation du DU plus ou moins importante.
Du coup la question est globalement quelle formule donne réellement une augmentation de 4,88 % ?
La différence n’est pas si insignifiante que ça en monnaie pleine, il me semble.
Edit :
J’ai fait une simulation avec Calc : Si je ne me suis pas planté, en prenant M/N à (t) on est bien proche de 4,88 % si on prend à (t+1) on est plus proche de 0.5 %. Finalement, on a le choix entre 9,997 % par an ou 10,25 % par an.
J’ai également fait mes calculs de mon côté pour déjà évaluer le taux de croissance de la Ğ1 connu jusqu’à présent. Basé sur les montants des DU.
| Date | Année | Montant DU |
|---|---|---|
| mars 2017 | 0 | 10.00 |
| sept 2017 | 0.5 | 10.01 |
| mars 2018 | 1 | 10.02 |
| sept 2018 | 1.5 | 10.04 |
| mars 2019 | 2 | 10.07 |
| sept 2019 | 2.5 | 10.11 |
| mars 2020 | 3 | 10.16 |
| sept 2020 | 3.5 | 10.23 |
| mars 2021 | 4 | 10.32 |
| sept 2021 | 4.5 | 10.42 |
c (mars 2017-sept 2021) = {{10.42 - 10.00 Ğ1} \over 4.5 ans} × 100 ≃ 9,33 % an
c ≃ 9,33%/ an ≃ 4,66 % / semestre
Donc, pour l’instant la Ğ1 est légèrement en dessous de la cible du taux de croissance fixé à 10 % par an ou 4,88 % par semestre.
En supposant que le montant du prochain DU soit de 10,52, ça donne :
c(mars 2017- mars 2022) = {{10,52 - 10,00Ğ1} \over 5 ans} × 100 = 10,4
Cette fois, ce serait légèrement au-dessus.