Question sur une asymétrie initiale due au DU(0)--Duniter

1

Je vous pose une question car je ne sais pas si c’est moi qui ai mal simulé le truc par rapport au fonctionnement effectif de Duniter, mais j’ai une question par rapport au DU(0) !

Je ne souhaite pas vous faire perdre du temps sur votre boulot, donc je vous poste ça comme ça, et suis conscient que tout post demande vérification de votre part. C’est la raison pour laquelle je vous envoie ce post en privé, mais je ne vois aucun problème pour qu’il soit publique.

Ceci étant dit:

Je voudrais savoir si l’erreur vient de moi ou s’il y a bel et bien un petit temps de “lancement” d’une monnaie qui contient une asymétrie.

Les membres initiaux d’une monnaie lancée par Duniter co-créent leur DU(0) qui visiblement est une valeur entrée lors du lancement, et la discussion sur le nombre de chiffre requis pour le DU est bien utile pour s’en rendre compte.

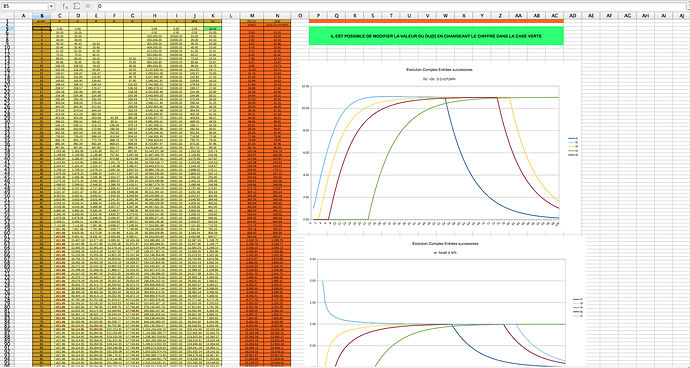
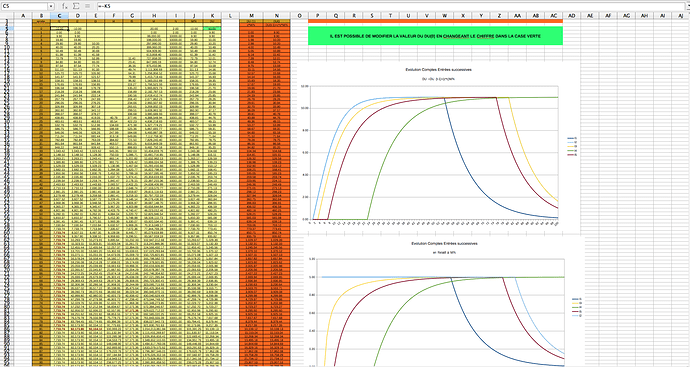
Du coup, voulant simuler le truc, nous nous retrouvons bien avec tous les premiers membres qui vont co-créer leur DU(0) et donc tous les membres à la moyenne, car ils auront tous 1 DU, et donc une division équivalente de la masse monétaire.

Ensuite, lorsque N va changer, en imaginant qu’un membre supplémentaire soit certifié, alors la moyenne (M/N) va baisser car N augmente.
Et là, dès la première entrée d’un membre, alors tous les membres initiaux se retrouvent avoir des comptes supérieurs à la moyenne, et donc entament un mouvement de convergence vers la moyenne “mais par le dessus” alors que le nouvel entrant, entame sa convergence mais “par le dessous”.

Et donc j’ai tenté de représenter ça pour m’en rendre compte et c’est en relatif à M/N que la différence est flagrante.

Quand les membres initiaux créent le premier DU(0), le fait qu’il le possède juste après les mets en avantage par rapport à M/N

avec DU0.png1859×992 404 KB

Mais si le compte des membres initiaux avant la création du DU(0) sont égales à -DU(0), alors ils arrivent à 0 lors de la création du DU(0), ce qui “gomme” un peu le problème.

Sans DU0.png1861×990 412 KB

C’est imparfait mais je voulais savoir si c’était moi qui était dans l’erreur ou si ce “problème” vous paraissait existant.

Assymetrie initiale1.5.ods (85,0 Ko)

2

C’est une interprétation mais elle est incorrecte du point de vue de la dimension de l’objet étudié.

Je t’invite donc à étudier ce fil initié par Anoa qui a fait un très bon travail d’analyse.

Et donc à élargir ton point de vue aux points de vue plus généraux qui sont que :

1°) Le nombre de DU moyen dans la monnaie n’est pas 1 DU / membre
2°) M/N(x) (la part de monnaie d’un individu) converge, pour tout membre présent ou futur, initial ou dernier, de la même façon par accumulation des DU, que l’on démarre à t=0 ou à t=120 doit produire la même analyse générale sans quoi on ne fait que démontrer que l’on a pas compris ce que signifie “symétrie temporelle”
3°) Réaliser le référentiel d’analyse correct où la moyenne correcte d’une monnaie libre est M/N = 1/c DU, et certainement pas “1 DU” ou “2 DU”, ou “4 DU” ou “x DU” selon le temps qu’il fait, et ainsi ne pas confondre “la moyenne à atteindre” avec “la moyenne à un instant t de quelques individus arbitrairement choisis”, que ce soient des individus initiaux, des individus(t), ou quelque ensemble particulier d’individus…
4°) Réaliser le module Galilée est un prérequis indispensable pour qui veut prétendre commencer à analyser correctement une monnaie libre, où il n’existe “ni premiers”, “ni derniers”.

2 Likes
4

Je vais regarder cela de plus prêt, mais la question ne se porte pas sur des éventuels “premiers” ou “derniers” dans n’importe quelle monnaie libre, la dessus je n’ai pas de problème à simuler leur évolution.

Il s’agit bien ici d’un problème concernant le démarrage d’une monnaie lancée par le biais de Duniter, dans lequel il y a bien des “membres initiaux” et un DU(0).

C’est bien évidement pour cela que je prends des pincettes car le “problème” constaté vient peut-être de mon tableur, et de ma compréhension du fonctionnement de Duniter.

Lors du lancement de la blockchain, les premiers membres co-créant tous leur DU(0) se retrouvent bien brièvement tous à la moyenne, ou j’ai raté un truc?

Du coup, c’est pour cela que je demande, car il n’y a pas symétrie dans mon exemple, mais concernant juste les “membres initiaux” ET dans le cas d’une monnaie blockchain lancée par Duniter.

Au sein du module Galilée, nous simulons une économie avec des comptes n’étant pas à 0, d’où ma remarque. Car c’est en essayant de reproduire ce que Duniter fait lors d’un lancement de monnaie que je me suis posé cette question, et ce problème n’est pas présent dans la simulation effectuée dans le module Galilée.

Je vais revérifier tout ça mais ça me pose question.

5

La “moyenne” considérée dans la symétrie temporelle n’a rien à voir en effet avec une moyenne de quelques individus. Les membres initiaux sont très loin de 1/c DU.

De quelle définition de la symétrie parles-tu ? Pour quel genre de monnaie ? Concernant quels prérequis ? De quoi parles-tu exactement ?

C’est faux, ceux qui ont réalisé le module Galilée ont parfaitement compris que tout membre démarre de 0 avec +1 DU au premier DU, et tous les membres rejoignant une monnaie libre au même instant démarrent bien tous avec une moyenne à 1DU, et ceci quel que soit “t”.

Il faut donc bien réaliser d’abord le module Galilée avant de pouvoir parler du sujet, la preuve est là.

Bien sûr que si. Et ce n’est pas un “problème”, tout ceci n’est qu’une conséquence de la forme d’une monnaie libre qui est la seule solution à la symétrie spatio-temporelle mise en évidence par la TRM. Il n’y a aucun “problème” ici mais uniquement le constat que la symétrie spatio-temporelle est bien présente partout, et en tout temps.

6

@Paulart Ce qui confirme ce que je t’ai dit vendredi : Les courbes vues en trois dimensions sont parallèles quelque soit le t de départ… :slight_smile:

7

Comme dit Galuel, si chaque membre de G1 produit 1DU par jour et que G1 a un taux de croissance de 0.026% par jour,
la moyenne où tous les comptes convergerons est de: 3846 Du (1/0.00026)

On est tous des nouveau entrant dans G1, donc même pour ses créateurs, il faudra environ 40ans pour atteindre cette moyenne (à échange équilibré).

8

Tortue a parfaitement expliqué le sujet, seul un contributeur ayant réalisé le module Galilée aurait pu répondre de façon aussi précise et complète.

J’ajoute que Ḡ1 a une croissance un peu différente, puisque le DU n’étant géré que sur 4 chiffres pour des raisons pratiques, il a été intégré un calcul biannuel et pas journalier avec c = 4,88% / équinoxe, qui est ensuite réparti en création de 182,625 DUjours égaux (moyenne de jours sur 4 ans contenus dans la période entre deux équinoxes).

Question : quelle sera la moyenne de convergence exacte de Ğ1 en DUjours !?

9

3 742,32 Du ?

10

Vérifions : 1/c * 182,625 = 1/(4,88%) * 182,625 = 3742,32 DU !

Yes !

1 Like