Bonjour,
Voici quelques suggestions/questions sur Cutecoin :
Bonsoir Sofrani,
et si tu passais en 0.10.1 
https://github.com/ucoin-io/cutecoin/releases/tag/0.10.1
Salut!
Je me demandais aujourd’hui pourquoi le dividende universel ne serait pas quotidien plutôt que mensuel?
Cela éviterait le stress des fins de mois difficiles de notre système actuel.
Il n’y a pas de raison ! uCoin permet cela d’ailleurs.
Il faut toutefois, afin de se faire une idée de ce dont il s’agit, préalablement répondre à la question : quel taux journalier correspond à un taux annuel de 10% / an ?
Vive les forums de maths 
http://www.ilemaths.net/forum-sujet-365867.html
Le taux journalier est de : 0,0261158 %
On peut le vérifier en calculant 1,000261158^365 = 1,1000000497457830360906315706825
On a bien 10% 
Excellent Nicos 
Tu aurais pu aussi trouver par : (1+10%)^(1/365) = 1,000261158 = 1 + 0,02611…%
D’où les deux questions complémentaires : Quel est le taux mensuel correspondant, ou le taux hebdomadaire correspondant ?
Et les questions subsidiaires : Dans le référentiel quantitatif, au bout de combien de temps la masse monétaire sera doublée, et au bout de combien de temps sera-t-elle multipliée par 10 ? Et dans le référentiel relatif que peut-on dire ?
Pour les 2 complémentaires, il suffit d’injecter 12 (mois) ou 52 (semaines) dans la formule soit:
Pour les subsidiaires:
!Excellent 
Eh oui, pas si simple. Je t’aide : il convient de réfléchir avec N constant (équivalent à “variant peu”) pour simplifier, et de constater que la masse monétaire ne bouge pas en relatif, donc on ne peut rien dire 
On peut par contre se demander au bout de combien de temps un individu ayant déjà produit x DU voit sa production doubler, en fonction de la valeur de x (par exemple si x vaut zéro, il n’y a pas de réponse).
Si le temps s’écoule de façon uniforme, les DU sont distribués de façon reguliere (tous les mois par exemple).
Donc si un individu a produit x DU en un temps T, il doublera logiquement sa production de DU également en un temps T ?
Imaginons qu’un individu ait produit x = 3/4 1/c DU, au bout d’un temps T. Selon ton affirmation au bout de 2T il aurait alors produit 2x = 3/2 1/c DU. Qu’en dis-tu ?
Non : si on considère le référentiel relatif (je l’ai mal appliqué) la production totale de DU par un homme plafonne à 1/c…
Si il est a 3/4 1/c , il ne pourra jamais doubler sa production, même en étant immortel!
En généralisant, Pour calculer dT tel que R(T+dT-to)=A.R(T-to) (avec donc A=2 dans ton exemple), Il y a une condition:
A<1/(1-exp(-c(T-to))
En posant R(t-To)=B 1/c (B=3/4 dans l’exemple)
Soit B=1-exp(-c(T-to))
La condition s’écrit :
A<1/B
Dans ton exemple 2>1/(3/4)=1,3333…
Donc il n’y aura pas de solution.
Si la condition n’est pas remplie, il n’y a pas de solution (l’égalité correspondrait à un humain immortel!)
Si la condition est remplie, j’ai calculé que :
dT=1/c (ln(1-B)-ln(1-AB))
J’espère que j’ai bon cette fois!
Donc un homme qui a produit x DU verrait sa production doubler au bout de :
1/c (ln(1-x)-ln(1-2x))
A condition d’avoir x<1/2
Dans le cas contraire elle ne peut pas doubler
Ca ne me semble pas clair, c’est peut-être juste, mais je vois mal la démonstration.
Etant donné que le nombre de DU produits à t alors x(t) = 1/c*[1-exp(-ct)], et nous cherchons “t” tel que x(t) = 2x(t0) (en posant x = x(t0) soit exp(-ct0) = 1 - cx ou encore t0 = -1/c ln(1-cx)) soit :
1/c*[1-exp(-ct)] = 2/c*[1-exp(-ct0)] => t = - 1/c ln(2 exp(-ct0) - 1) = -1/c ln(1-2cx) et donc pour connaître t-t0 :
t-t0 = -1/c ln(1-2cx) - (-1/c ln(1-cx)))
t-t0 = 1/c*(ln(1-cx) - ln(1-2cx)
Ce qui ressemble exactement à ta solution, mais avec “cx” à la place de “x” tout seul, la solution impliquant que x doit être strictement inférieur à 1/2 1/c. Ceci étant une question de notation, expliqué par le fait que tu as choisi de donner à x une valeur “fraction de c”, et pas un “nombre de DU” exprimé en fonction de “c”, pure question de convention.
A noter toutefois que pour être complet cela ne suffit pas ! Car il faut que la solution soit aussi inférieure à l’espérance de vie pour “t” pour prétendre connaître le cas général (quoique pour un individu particulier on puisse aller au delà de “ev”, il nous faut tout de même garder en tête la limite moyenne de vie et connaître les solutions qui s’y rapportent) Donc il faut poursuivre :
t = -1/c ln(1-2cx) < ev => x < 1/2 1/c [1 - exp(- c ev)]
Qui est une condition plus forte que la précédente. Par ailleurs si on note que c = ln(ev/2) / (ev/2), alors cela se simplifie encore par :
x < 1/2 1/c [1 - exp( - 2 ln(ev/2)] soit x < 1/2 1/c [1 - 1/(ev/2)²]
Il s’ensuit qu’un individu ayant déjà produit “x” DU verra sa production doubler au bout de :
t-t0 = 1/c*[ln(1-cx) - ln(1-2cx)] = 1/c ln[(1-cx)/(1-2cx)]
Sous condition que x < 1/2 1/c [1 - 1/(ev/2)²] pour des individus de durée d’espérance de vie moyenne “ev”, avec c = ln(ev/2)/(ev/2)
Il n’y a plus qu’à réaliser des graphes de ces fonctions et à les commenter pour en faire un joli nouveau petit théorème TRM que tu pourras signer de ton nom ! 
Correction : x=B/c
En appliquant la formule du post précédent , la formule du temps de doublement du nombre de DU , en partant d’un portefeuille de x DU, est :
1/c (ln(1-cx)-ln(1-2cx))
Merci a Galuel !
Dans ce cas on a b = cx, et en remplaçant on aura qu’un individu ayant déjà produit "x = b/c " DU à la date t0 verra sa production doubler au bout de :
t-t0 = 1/c [ln(1-b) - ln(1-2b)] = 1/c ln[(1-b)/(1-2b)]
Sous condition que b < 1/2 [1 - 1/(ev/2)²] pour des individus de durée d’espérance de vie moyenne “ev”, avec c = ln(ev/2)/(ev/2).
Ca marche, je suis en tain d’étudier cette fonction et voir en quoi elle peut être utile!
Whaouu zetes pas mauvais en math on dirait…
J’ai tracé pour c compris entre 5% et 20% la fonction
f(x)=1/c [ln(1-cx)-ln(1-2cx)]
On peut dire que :
On voit donc que le doublement du nombre de DU produits prend de plus en plus de temps jusqu’à devenir très élevé quand x=1/2 1/c (1-1/(ev/2)²) puis simplement impossible.
Pourquoi calculer le temps du doublement? (interprétation):
Un individu dépense seulement les DU qu’il produit. Son portefeuille arrive à 0 au bout d’un temps T0, au cours duquel il a produit x0 DU. Il se demande alors si les DU qu’il va produire à l’avenir vont lui permettre de continuer à vivre de la même façon. Pour celà on calcule le temps T1 nécessaire au doublement , pour le comparer à la première période T0.
Les courbes montrent que T croît avec x, donc T1>T0. Petit à petit, il doit donc se serrer la ceinture.
(1) Pour x petit (initialisation du portefeuille) : f(x)#x, donc T1#x0#T0 (car le nombre de DU cumulés est proche du nombre d’unités de temps pour les produire). On a donc T1#T0.
(2) Plus x augmente, plus le T nécessaire au doublement croît fortement et l’égalité (1) n’est plus vérifiée.
(3) Pour x>1/2c, il n’est plus défini : il ne pourra plus jamais vivre comme au début, avec seulement ses DU. Il devra donc travailler, échanger des valeurs qu’il produit avec les autres membres de la communauté…
Mais je ne vois pas de théorème à l’horizon!
Peut-être un résultat approximatif quand même : on ne peut pas vivre seulement de ses DU. Sachant que dans la TRM, on ne peut pas définir ce qui est nécessaire à la vie!
Puis ensuite :
Il me semble qu’il y a une erreur de raisonnement.
En effet si un individu est à 0, qu’il ait ou non produit x0 DU préalablement, le temps nécessaire pour produire x0 nouveaux DU sera le même, et ne dépend absolument pas de ce qui s’est passé préalablement.
L’hypothèse et le raisonnement me semblent donc à revoir
Ayant bien retenu l’histoire de Galilée, quand on a du mal à comprendre ou à modéliser quelquechose, il faut penser à…changer de référentiel! Je passe donc au référentiel quantitatif, et je cherche à répondre à la question suivante :
A quoi correspondrait, dans le référentiel quantitatif, une multiplication par 2 du nombre total x des DU déjà produits ?
Il faut donc calculer le coefficient K tel que : Q(t+T-to)=K.Q(t-to)
où T est le temps tel que x(t-to+T)=2x(t-to) , x en relatif.
Pour mémoire :
T=1/c ln[(1-cx)/(1-2cx)]
x(t-to)=1/c [1-exp(-c(t-to))] , ou encore [1-exp(-c(t-to))]=c.x(t-to)
D’après le §5 de la TRM, en quantitatif, la somme des unités monétaires produites entre to et t est : Q(t-to)=(M/N)(to) exp(ct) [1-exp(-c(t-to))]
Donc Q(t-to)=(M/N)(to) exp(ct).c.x(t-to)
Et Q(t-to+T)=(M/N)(to) exp(c(t+T)).c.x(t-to+T)
Or x(t-to+T)=2x(t-to), et exp(c(t+T))=exp(ct).exp(cT)
On a donc
Q(t-to+T)=(M/N)(to) exp(ct).exp(cT).c.2.x(t-to)=2.exp(cT).Q(t-to)
Donc :
K=2.exp(cT)
Soit K=2.[(1-cx)/(1-2cx)]
En remplaçant le doublement par une multiplication par 1, et donc les 2 par des 1, on trouve K=1, donc ça me paraît bon !
Je propose donc une règle de conversion du relatif au quantitatif.
Voici ce que serait mon théorème 
:
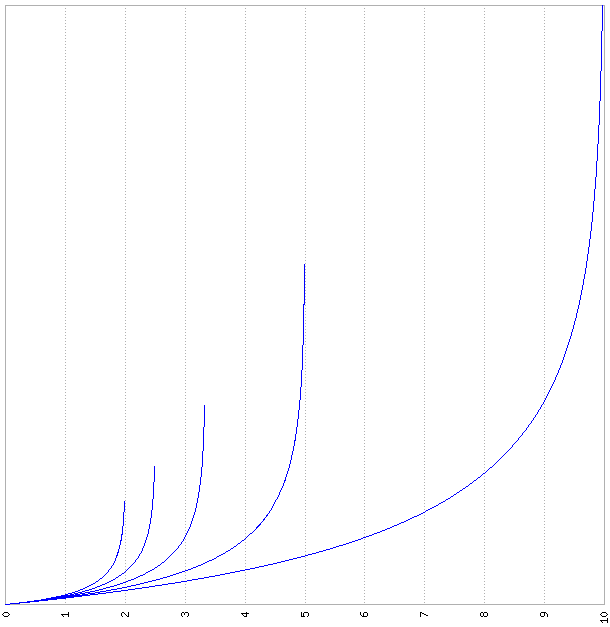
A condition d’avoir x<(1/2c), le doublement du nombre x d’unités relatives co-produites par un individu équivaut à la multiplication de la somme des unités monétaires co-produites par un facteur égal à : 2.[(1-cx)/(1-2cx)].
On peut remplacer le facteur “2” par un autre nombre (en remplaçant tous les 2), pour généraliser.
Resterait à trouver la relation inverse (du quantitatif au relatif), et étudier les propriétés de ces fonctions.
