Pour compléter le fil traitant de l’étude du nombre de chiffres requis pour le DU et qui a aboutit au calcul tous les 6 mois du nouveau DU, voici un complément mathématique amusant pour à l’inverse choisir la période de x jours de calcul du DU que l’on voudrait trouver et qui correspondrait à l’augmentation du DU journalier de 1 centime.
Il faut faire attention dans ce calcul à comprendre que le DU calculé l’est comme la somme totale de la prochaine période de x jours à suivre, et qu’il faut donc diviser le montant trouvé par x pour estimer si le DU journalier sera augmenté de 1 centime, on cherche donc au final une période de x jours où le DU calculé sera un DU journalier cumulé sur la période augmenté de x centimes.
Les bases :
- DU(t+1) = DU(t) + c² (M/N)
- c = 10% / an = 10% / 365,25 jours
On veut donc chercher une augmentation qui soit équivalente, soit un cx = x% / jour tel que (1+cx)^(365,25/x) = 1+c soit :
- cx = (1+c)^(x/365,25) - 1
On veut donc que DU(t+1) - DU(t) = 0,01 * x, ce qui nous conduit à :
- cx² (M/N) = 0,01 * x => cx² = 0,01 * x / (M/N)
Et donc vient l’équation à une seule inconnue x, impossible à résoudre exactement avec les fonctions usuelles :
- (1+c)^(x/365,25) - 1 = cx = [0,01 * x / (M/N)]¹/²
Que l’on peut transformer en :
- x = ln [1 + [0,01 * x / (M/N)]¹/²] * 365,25 / ln(1+c)
Toutefois comme M/N est plutôt grand, 0,01 petit, que l’on sait que x ne sera pas très grand (plus petit qu’un an, de quelques jours à 100 ou 200 jours), on peut estimer que le terme [0,01 * x / (M/N)]¹/² restera petit.
On sait que lorsque x est petit on a ln(1+x) ~ x, ce qui va nous donner une très bonne solution approchée (sinon on teste toutes les valeurs de x, de 1 à 365 jusqu’à trouver la bonne valeur numérique) :
- x = [0,01 * x / (M/N)]¹/² * 365,25 / ln(1+c)
Après avoir tout mis au carré on extrait enfin la jolie formulation :
- x = 0,01/(M/N) * [365,25 / ln(1+c)]² (A)
Ce qui nous donne pour c = 10% / an la formule très simple :
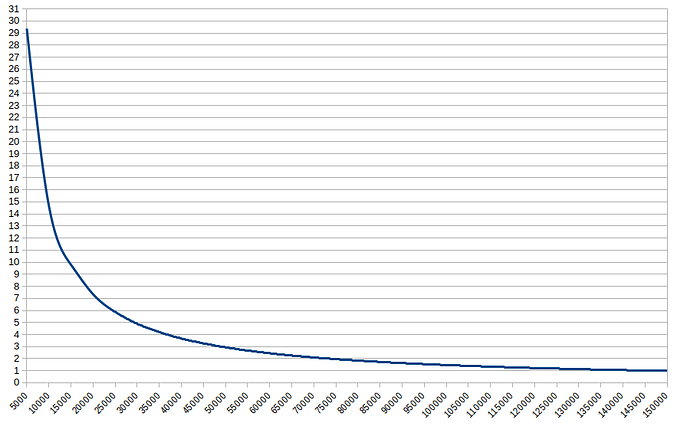
- x = 146860 / (M/N)
A.N.
Si M/N atteignait la monnaie pleine à 37000 Ğ1 / membre on obtiendrait p = 4 jours
Avec M/N = 1920 Ğ1, on obtiendrait b = 77 jours
En pratique, un algorithme qui utiliserait l’approche de la période à calculer prendrait le bloc du dernier calcul du DU en référence, et inclurait dans ce même bloc le résultat du calcul de la période de revalorisation suivante, en donnant directement le numéro du futur bloc dans lequel le prochain calcul de période se fera, le DU étant alors revalorisé sur chacun de ces blocs de 1 centime exactement.
Toutefois le procédé ne serait pas aussi simple dans le temps, puisque M/N augmentant, le DU suit, et l’augmentation de 1 centime devient de plus en plus petite, donc devra se faire de plus en plus rapidement, au delà de 150 000 Ğ1 la période x deviendrait inférieure à 1 jour et continuera de tendre vers zéro…
Ceci implique qu’il faut calculer la période non pas sur une quantité de 1 centime, mais sur un % du DU, par exemple 0,1 % DU, ce qui est facilement réalisé en remplaçant dans la formulation finale 0,01 par 0,1% DU, car les calculs ne changent pas, le DU étant petit devant M/N :
- x = 0,1% DU / (M/N) * [365,25 / ln(1+c)]² (B)
Et avec cette formulation, la période de calcul convergera vers 40 jours par valeurs supérieures (puisque DU / (M/N) convergera lui même vers 10/3700 par valeurs supérieures).
– A noter qu’à inverse on peut aussi trouver l’augmentation “a” du DU journalier correspondant à une période x donnée, on obtient alors :
- a = x*(M/N) / [365,25 / ln(1+c)]²
Ce qui pour x = 182,625 jours et M/N = 1920 Ğ1 nous donne 2,4 centimes, ce qui correspond aux calculs actuels de la Ğ1 à la date du jour.