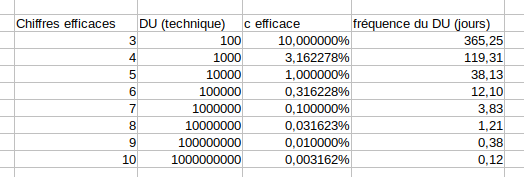
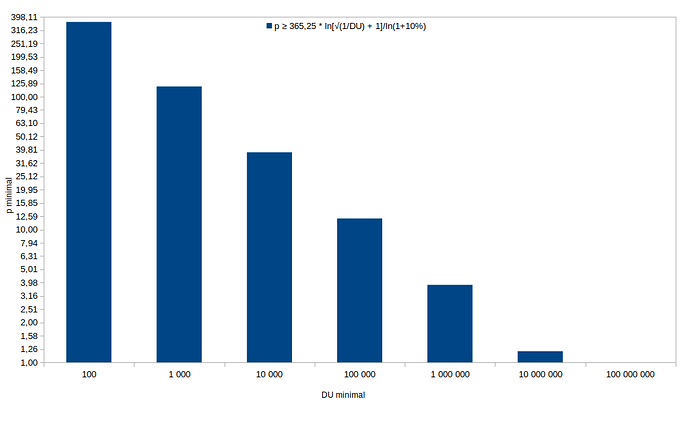
Etant donné le constat expérimental qui va au centime utilisé dans d’autres monnaies, ayant un nombre de digits de 9999,99 maximum par mois très largement suffisant pour un DU mensuel efficace, soit 6 digits / mois on peut calculer le nombre de chiffres requis pour un DU selon la période de temps considérée :
- DU mensuel : 9999,99 soit 6 chiffres suffisants.
- DU annuel : 9999,99 x 365,25 = 3652496,34 soit 9 chiffres suffisants (mais fréquence hors sujet)
- DU journalier : 9999,99 / 30 = 333,33 soit 5 chiffres suffisants
- DU horaire : 9999,99 / 30 / 24 = 13,88 soit 4 chiffres suffisants
Pour des raisons de contrôle humain d’une part, et de quasi-continuité d’autre part, la journée semble bien être l’unité de mesure la plus appropriée pour la génération d’un DU, qui peut donc suffire avec 5 chiffres efficaces.
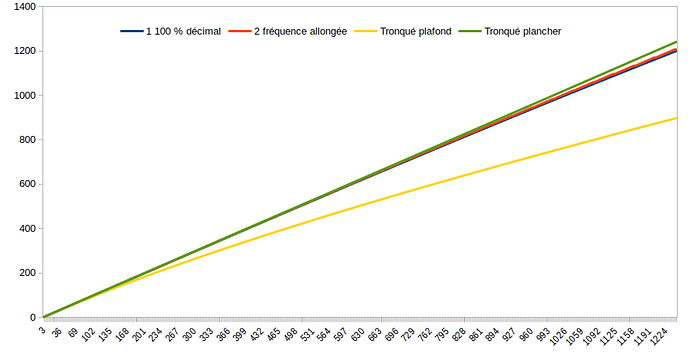
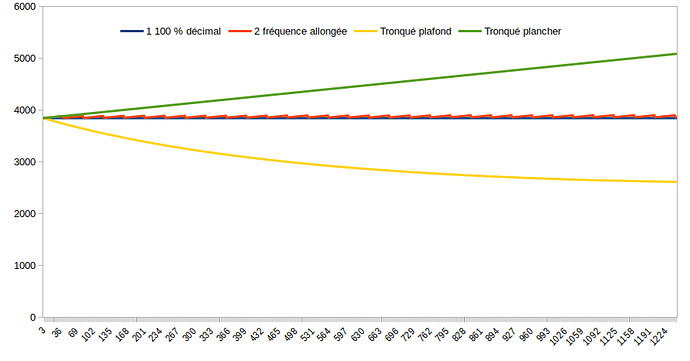
Par ailleurs le passage en roulement de puissances de 10, peut le faire dépasser 5 chiffres, pour retomber sur 5 :
- DU(0) = 100,00
- DU(1) = 110,00
- …
… 25. DU(24) = 984,97
… 26. DU(25) = 1083,47 = 108,35 puissance de 10 : 1
… 249. … … puissance de 10 : 9
… 250. … … puissance de 10 : 1
Tous les 25 ans x 10 = 250 ans, on peut y compris faire tourner la puissance de 10, sans besoin de stocker donc des nombres en expansion nulle part.
Sur le taux : il faut calculer la précision du taux cible en fonction du nombre de décimales efficaces.
Ainsi pour c = 10% / an, le taux journalier correspondant est : c = (1 + 10%) ^ (1/365,25) - 1 = 0,0260979 % / jour
Mais étant donné qu’on aura 5 chiffres pour le DU, calculons à au plus 6 chiffres pour vérifier la précision :
- 999,99 x (1+0,0260979 %) = 1000,25
- 999,99 x (1+0,026098 %) = 1000,25
- 999,99 x (1+0,0261 %) = 1000,25
- 999,99 x (1+0,026 %) = 1000,24999 = 1000,25
- 999,99 x (1+0,03 %) = 1000,29 la différence devient sensible au centime près.
La précision du taux à 0,026% / jour est donc suffisante. Cela donne la même exactitude que de prendre plus de décimales pour le taux trop précis de 0,0260979% qu’il est donc inutile d’utiliser.
La simple remarque que 0,026% = 0,00026 comporte 5 décimales après la virgule et donc impacte les 5 chiffres du DU à la dernière décimale eût suffit à réaliser le même constat.