Voici un nouveau descriptif de la croissance de la toile de confiance de la monnaie libre Ğ1 en cette fin d’année.
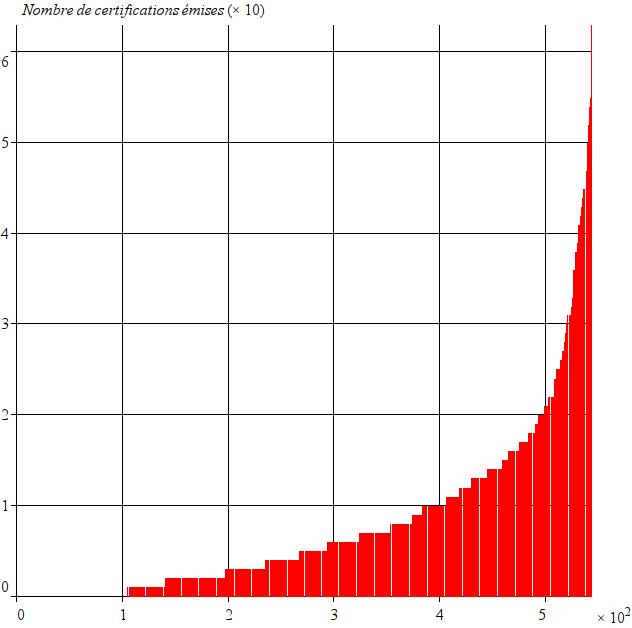
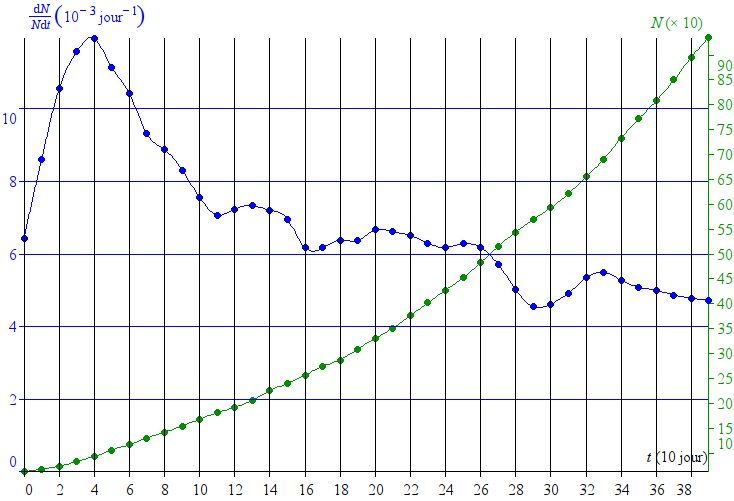
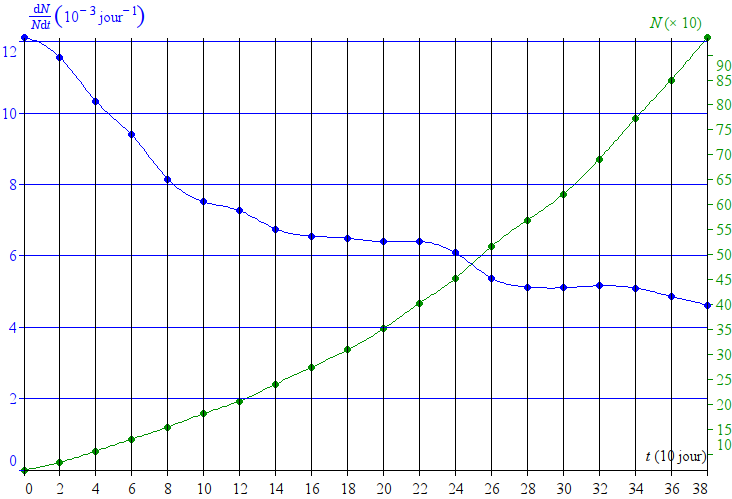
On peut d’abord se demander quels sont les membres qui font croître la toile par leurs certifications. On pourrait penser que tout le monde contribue à peu près de la même façon, ou, au contraire, certains plus que d’autres. Traçons le nombre de certifications par membre, du moins au plus actif :
On voit que tous les membres sont loin d’émettre le même nombre de certifications. Sur 544 membres, plus d’une centaine, par exemple, n’en a pas émis encore une seule, alors que le membre le plus actif (je ne donnerai pas de nom) en a déjà fourni 63 sur les cent dont il dispose.
On peut remarquer qu’en choisissant parmi les certificateurs les plus actifs, 15% des membres ont émis la moitié des certifications, et 50% en ont émis 90%.
Conclusion : la croissance de la toile est due essentiellement à une petite fraction de l’ensemble des membres. Si l’on rapproche ce fait du délai minimal de cinq jours entre deux certifications successives, on comprend que :
- au début de la monnaie, lorsque la toile comprend peu de membres, la croissance est linéaire dans le temps (affine pour être plus précis) puisque ce sont toujours pratiquement les mêmes membres qui certifient ;
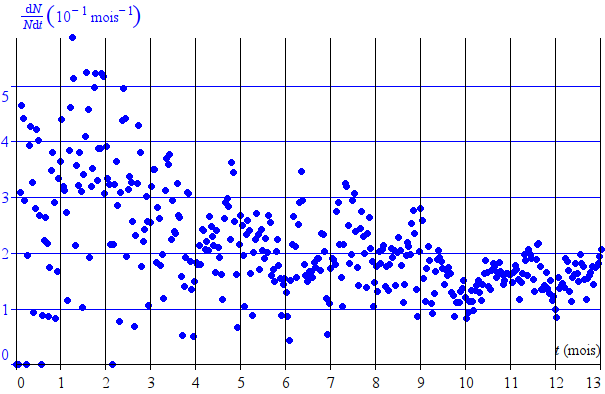
- par la suite, un excédent de certificateurs permet un nombre d’entrées par unité de temps proportionnel au nombre de membres, avec un coefficient de proportionnalité chaotique du fait de la faible proportion de certificateurs ; cela permet d’observer une croissance exponentielle de la toile, mais avec beaucoup de perturbations (un physicien dirait : beaucoup de bruit) autour de la courbe idéale.
Pour préciser la méthodologie utilisée pour mesurer les données, l’origine des dates correspond au lancement de la monnaie (08/03/2017 15:32:07), les durées entre les dates correspondent à celles du temps usuel, données par le champ “time” de la table “block” de la base de données de Duniter, et non par le champ “medianTime”, couramment utilisé par ailleurs. Le nombre de membres est mesuré pour chaque période de 24 heures à partir de l’origine, ce qui correspond à un point sur les graphiques suivants.
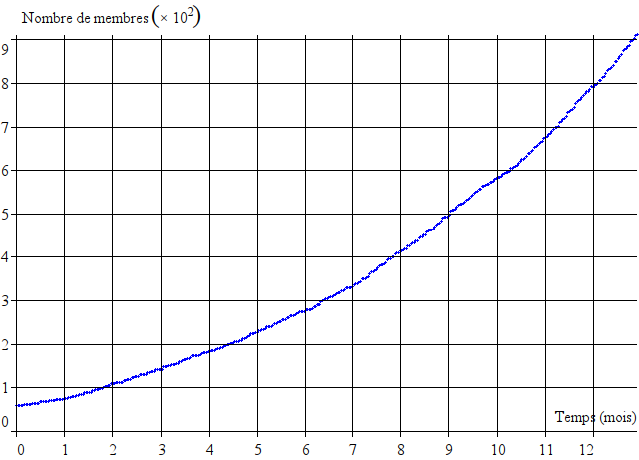
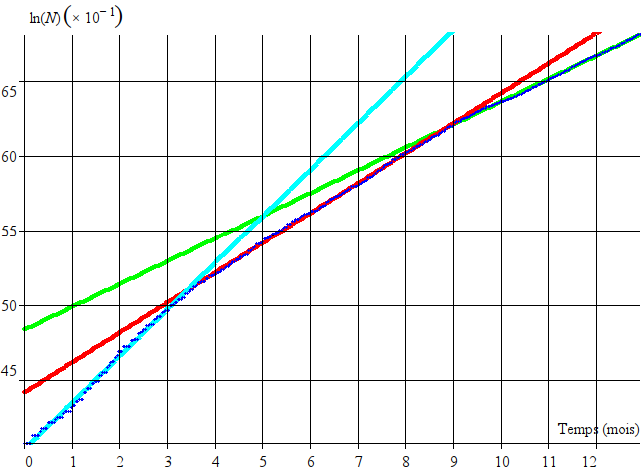
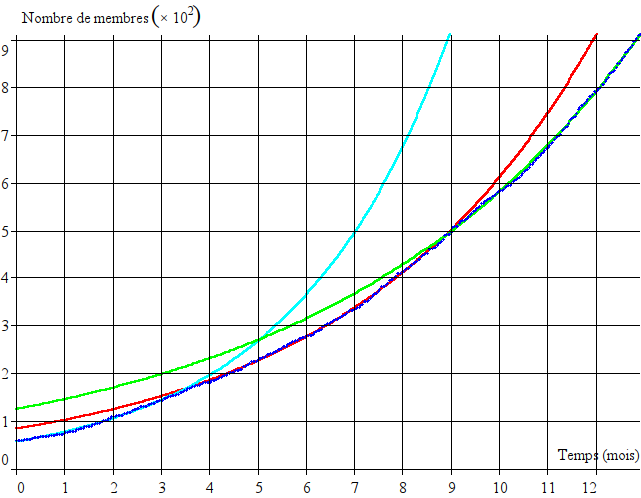
Voici d’abord les données brutes :
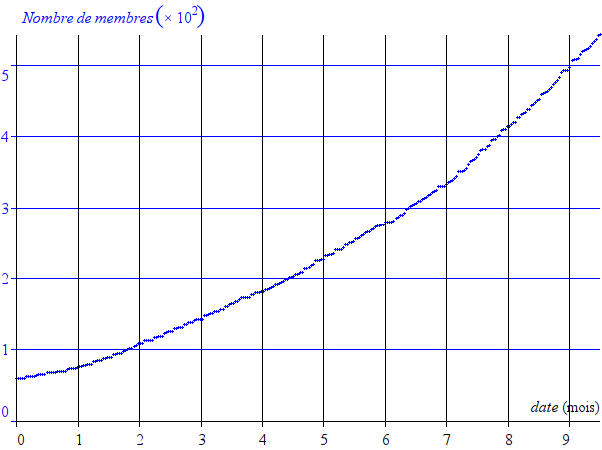
On peut remarquer une première partie affine, à faible pente, d’une durée d’un peu plus d’un mois, suivie d’une deuxième, à pente plus forte, jusqu’à, environ, quatre mois et demi. Ensuite, une courbe (exponentielle) commence à se former jusqu’à aujourd’hui. On peut donc chercher un modèle de la forme :
if t < tL1 then
a1 * (t - tL1) + a2 * (tL1 - tL2) + N0 * e ^ (c * tL2)
else if t < tL2 then
a2 * (t - tL2) + N0 * e ^ (c * tL2)
else
N0 * e ^ (c * t)
où t est le temps, tL1 la date de la rupture de pente des deux parties affines, tL2 la date du début de la dernière partie (exponentielle), a1 est la pente de la première partie, a2 celle de la deuxième, N0 est la valeur qu’aurait l’exponentielle à t = 0, et c est le taux de croissance de l’exponentielle. L’expression de la fonction a été choisie pour qu’elle soit continue en tout point. Curieusement, elle apparaît également différentiable, en première approximation, en tL2.
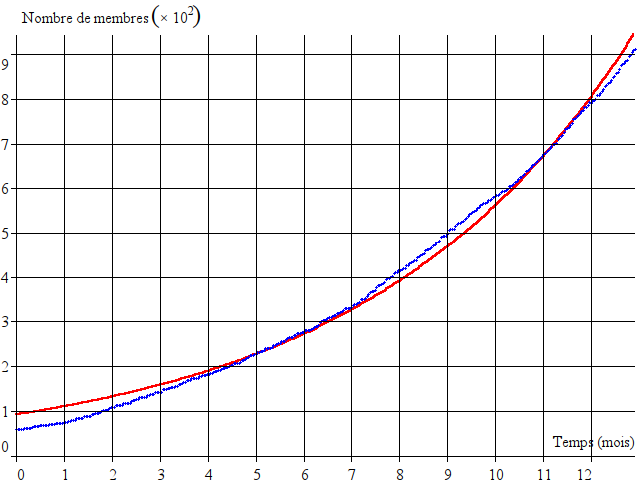
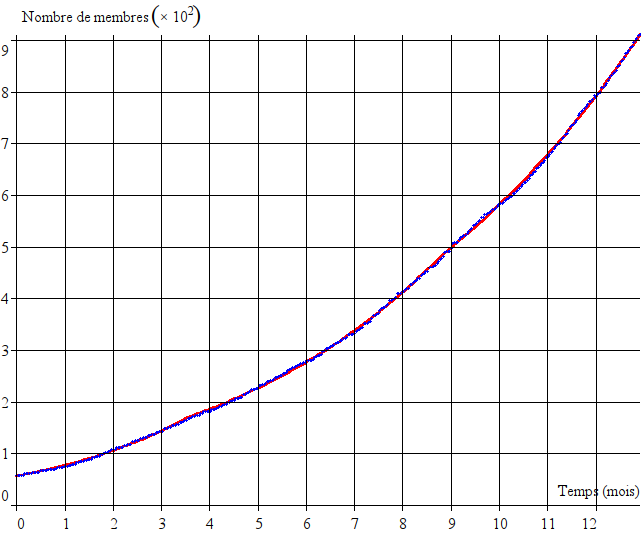
On ajuste ensuite les paramètres tL1, tL2, a1, a2, N0 et c par la méthode des moindres carrés (Méthode des moindres carrés — Wikipédia) de façon à ce que la courbe passe le mieux possible entre les points. On obtient ceci :
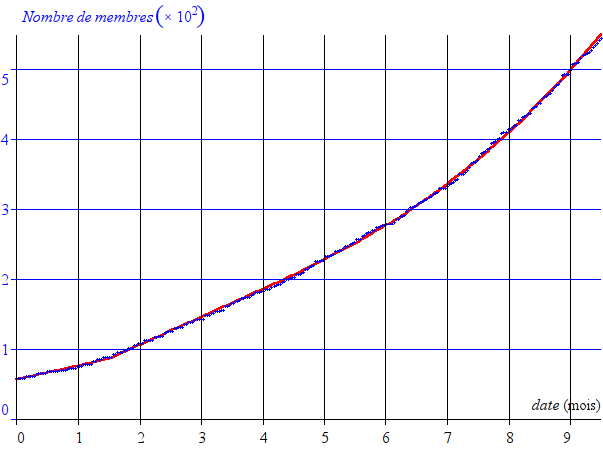
On observe que les points suivent assez bien la courbe, malgré quelques fluctuations.
L’écart moyen entre les points et la courbe (écart-type) est de 2,5 membres.
Les paramètres ont pour valeurs :
tL1 = 1,496 +/- 0,096 mois
tL2 = 4,4 mois (peu précis)
a1 = 19,8 +/- 1,8 membres / mois
a2 = 39,81 +/- 0,46 membres / mois
N0 = 85,02 +/- 0,49 membres
c = 19,674 +/- 0,075 % / mois
La dernière valeur, qui est le taux de croissance de la dernière partie, exponentielle, est la plus intéressante. Elle indique que le nombre de membres de la toile de confiance augmente de 19 à 20 % par mois, de façon régulière pour l’instant. Ce taux, extrapolé à l’année, correspond à un décuplement (e ^ (c * 12) = 10,6) du nombre de membres. Restons toutefois prudent, car il peut subvenir à tout moment des évènements qui infléchissent cette croissance, sans oublier que l’action future de la règle de distance deviendra à terme prédominante. Il n’en reste pas moins que la vitalité de notre toile est impressionnante.
Joyeuses fêtes et bonne année.