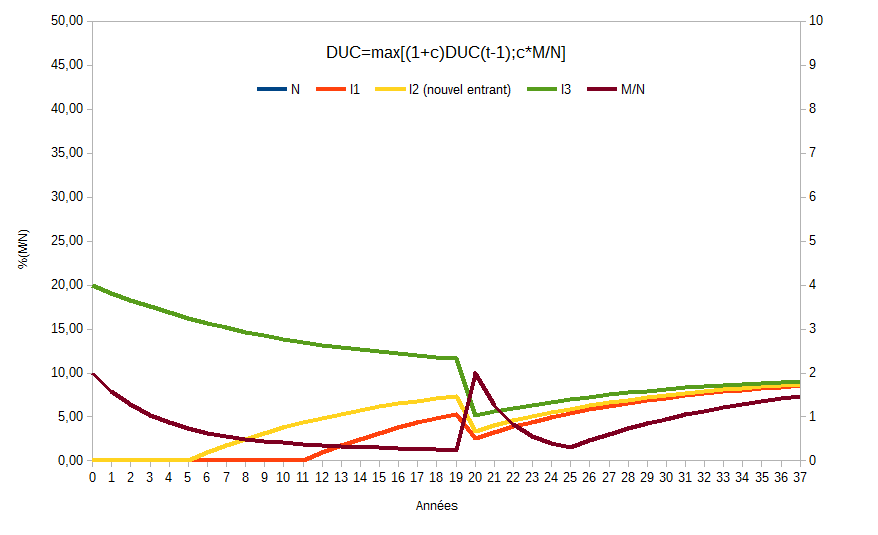
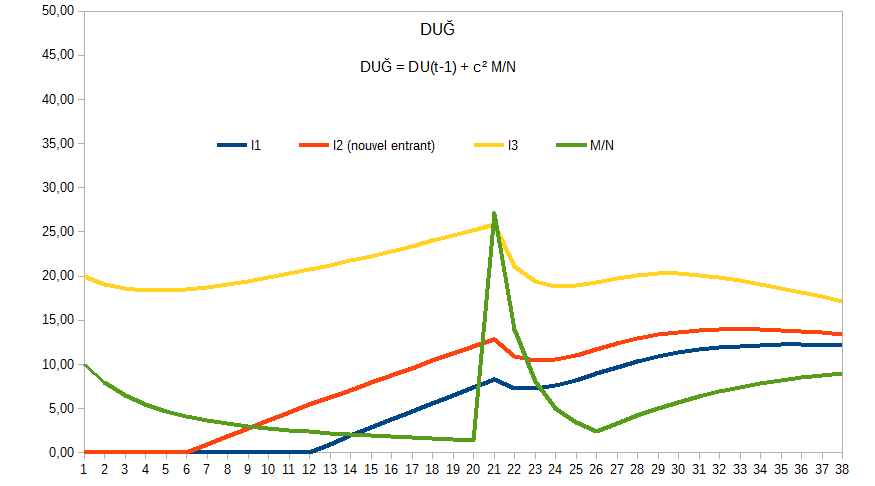
Les graphes du fichier DUABCĞ-DU.ods sont biaisés car le DU(t = 0) ne correspond pas vraiment à c*M/N mais plutôt à (c/2)*M/N, et puis le graphe DUB avait un M/N initial du double du M/N des autres graphes, donc la comparaison graphique était faussée.
Mais globalement les tendances restent identiques, on pourra toutefois noter :
- une chute étrange à t = 1 qui disparaît, et donc des variations moindres entre [t = 0 ; t = 19 ]
- dans DUB, I3 reste bien à 10%, ce qui était bien le but d’@Anoa pour cette formule
Les revoici donc : DUABCĞ-DU_revise.ods (70,8 Ko)
Bon après, effectivement la formule DUG est quand même moins “montagnes russes” que DUA tout en tenant compte de N, et cela sera peut-être utile pour les forts mouvements que l’on risque de connaître au lancement d’une monnaie libre (forte hausse de membres due à l’initialisation, ou même chute à cause de bugs ou de pressions extérieures).
C’est marrant, en voyant ces courbes j’ai l’impression de revenir en cours d’automatique avec les régulateurs PID.