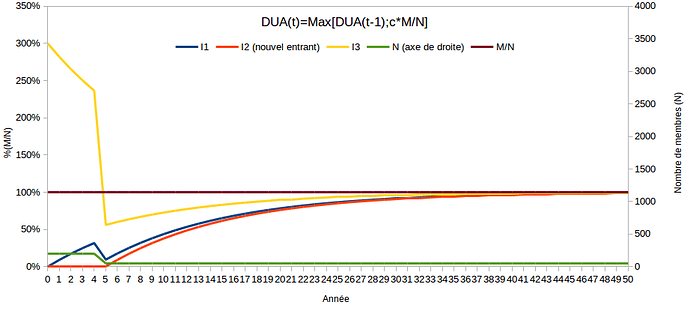
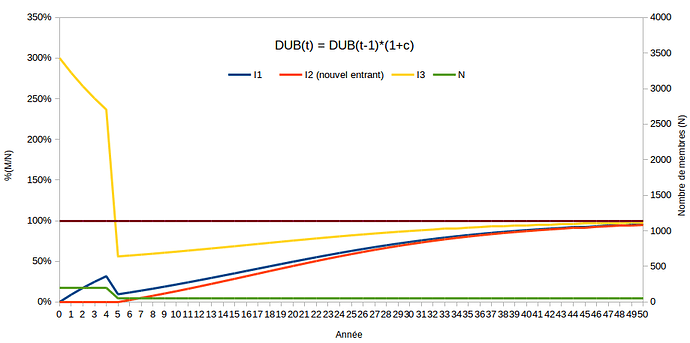
Afin d’aider à la progression j’ai réalisé un tableur que voilà (MAJ 13:25 plus facile à gérer sur une seule feuille) : DUAB.ods (61,6 Ko)
Notamment quand N augmente on remarque visuellement que les deux solutions sont très proches (il faut calculer avec une métrique pour voir la légère différence, et ne pas se contenter de regarder la différence entre un compte DUA et DUB, mais regarder la convergence des écarts entre les comptes hauts et les comptes bas de chacun des DU !).
C’est pour N qui chute vers le bas (ici de 200 à 50 membres) que l’on voit visuellement la différence entre entre DUA et DUB : tandis qu’avec DUA un compte bas converge avec une forme exponentielle, DUB suit une convergence linéaire. Ce qui induit un écart de convergence significatif.
Il faut noter ici d’un point de vue général et mathématique :
- En cas de N variable, pour visualiser correctement la monnaie il vaut mieux compter en % de la moyenne M/N pour mieux voir la position relative des courbes.
- Des couleurs et légendes précises permettent d’y voir mieux
- DUA est supérieure pour la raison qu’elle assure la continuité de la valeur relative du DU, c’est à dire de la dérivée. Tandis que DUB n’évite pas un effondrement de sa valeur relative ! Car sa formulation ne tient justement pas du tout compte de M/N dans son calcul ! Donc une forte discontuinité de M/N n’impacte pas son fonctionnement, ce qui crée ce qu’on appelle un DIRAC. Le seul auditeur à avoir compris ce point immédiatement était présent aux Roumics de Lille de Janvier 2014.
- Une métrique précise est nécessaire pour chiffrer les différences d’écart de convergence (qui donnent une bonne image du pouvoir d’achat relatif entre comptes “riches” et “nouveaux entrants”). C’est rapide et facile à faire une fois qu’on a fait tout ce qui précède (ex : Somme de (I3-I1) de t=5 à t+45).
- On peut envisager de trouver mieux que DUA, mais attention à ne pas chercher que pour des cas de variations de N(t) uniques et limités, il faut comparer dans une pluralité de cas (plusieurs variations soudaines, à la hausse comme à la baisse… variations continues… variations discontinues)…
- Il n’existe pas de formule “absolument bonne” car on pourra toujours trouver des variations de N(t) spécifiques qui donneront un avantage à l’une ou l’autre des optimisations possibles. Il s’agit donc de trouver une bonne formule valide dans la plus grande majorité des cas, et qui résiste bien. Si en plus sa formulation est simple, c’est idéal. DUA est très simple, et on voit visuellement immédiatement la présence de la dérivée précédente et de c et M/N, qui assure le fait qu’elle prend tout en compte pour optimiser.