J’ajoute des courbes gris clair pour comparer avec la normale (N stable).
Bosse: DUA est le plus proche de la normale. DUB est le plus loin mais il décale toutes les courbes, alors que DUC semble trop avantager les nouveaux arrivants.
Trou: I2 est clairement le grand vainqueur dans DUA et DUC. Comme pour la bosse, il me semble qu’ici aussi DUC avantage trop les nouveaux arrivants.
N(t) plus cahotique : DUABC.ods (114,7 Ko)
DUB ne semble pas si mal finalement, et ne génère qu’un écart acceptable pour une formulation plus simple et plus facile en terme de communication.
On pourrait donc la choisir pour sa simplicité et sa conformité dans plusieurs cas avec ce qui est attendu. Je penche en faveur de DUB pour ces raisons là, à moins qu’on ne démontre des cas de N(t) qui la déligitimeraient trop.
Il y a quand un même I2, le nouvel entrant, qui atteint beaucoup plus vite M/N dans le cas de DUA par rapport à DUB.
En plus, je ne trouve pas la formule DUA si compliquée que ça à communiquer : le DU est juste au moins égal au précédent !
Dans ce cas précis oui, mais en quoi est-ce un critère de légitimité ? Dans ce cas avec un DU = 99% M/N on atteindra aussi M/N rapidement, donc dit comme ça, on a pas d’information sur la légitimité. Il faudrait estimer précisément lequel des cas est le plus légitime.
Disons que DUB est encore plus simple, le DU étant parfaitement prévisible dans le temps, sans inconnue, et sa formulation hyper simple. Dans les cas de N variant peu, on ne verra pas la différence, elle sera vraiment faible, et même dans ces cas de variations fortes, l’écart n’est pas si grand.
A la fin il faut se dire que ces solutions sont proches, et que ce n’est pas forcément la plus précise techniquement qui sera la plus précise socialement. On peut se dire que l’adoption d’un principe général est facilité par une présentation la plus simple possible, et que le coût de présentation pourrait se voir compensé par le coût de la précision.
Faut-il avoir la formulation la plus précise, qui soit comprise par 1000, ou bien la formulation la plus simple, moins précise mais pas non plus infiniment éloignée, qui soit comprise par 10 000 ? On est en droit de se poser la question.
Ce qui compte surtout ici c’est de prendre la mesure de ces différentes dimensions : écart acceptable relativement à l’optimum, simplicité, clarté, communication, adoption, coût de formation…
Cas d’initialisation d’une monnaie libre, entrée de nouveaux entrants successifs 1, puis 2, puis 3 (100% puis 50% d’augmentation de N). DUABC.ods (94,4 Ko)
Voici pourquoi je n’utiliserai pas DUA dans la monnaie que je veux mettre en place :
Les variations de N (U sur mes graphes) perturbent la convergence des comptes relatifs vers la moyenne normale 1/V. Or pour rendre les choses simples, j’exprimerai les comptes en relatif avant tout, plutôt qu’en quantitatif, et je ne me vois pas expliquer aux utilisateurs que leur compte converge vers 1/V seulement si le nombre d’utilisateurs reste stable. A mon avis ils penseraient que leur compte leur échappe, puisque ça peut monter ou descendre de manière imprévisible.
Les potentiels d’achat s’éloignent beaucoup de la normale (N stable) lorsque N augmente de manière forte et durable.
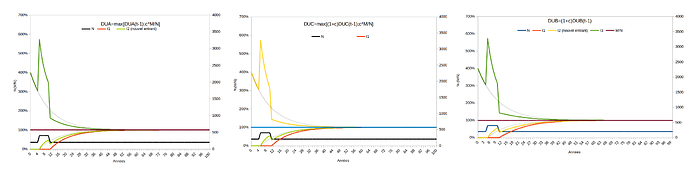
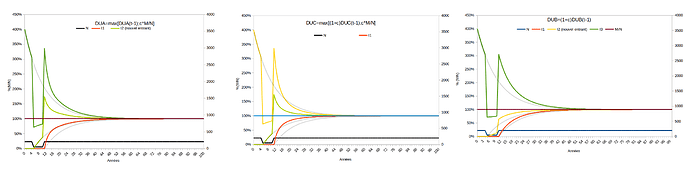
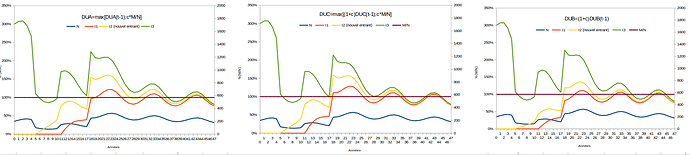
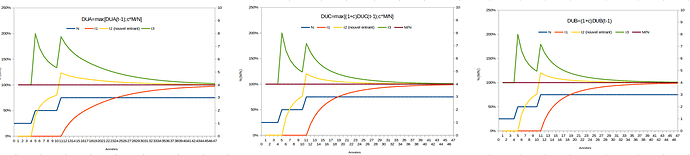
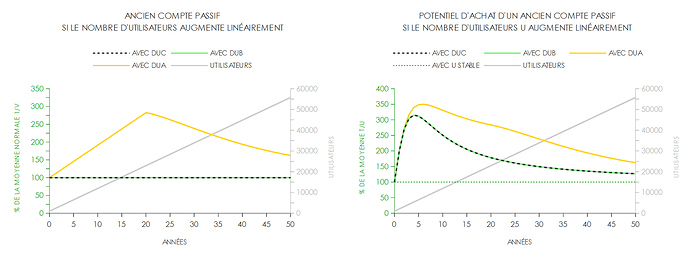
Non c’est faux. Le potentiel d’achat ne se compare qu’au sein d’une même monnaie, et est un % de M/N, toute autre définition est incorrecte, car d’autres monnaies ont des variations de prix les unes par rapport aux autres. Donc faire cette comparaison sur un même graphique porte à confusion, il faut en faire un par monnaie, laquelle monnaie doit surtout comparer anciens et nouveaux dans le temps (donc l’espace-temps interne à la monnaie).
Donc tu devrais comparer par rapport à M/N, ce qui est un premier point très important en terme de “potentiel d’achat”, car c’est ainsi que c’est défini, et que le sens a été défini.
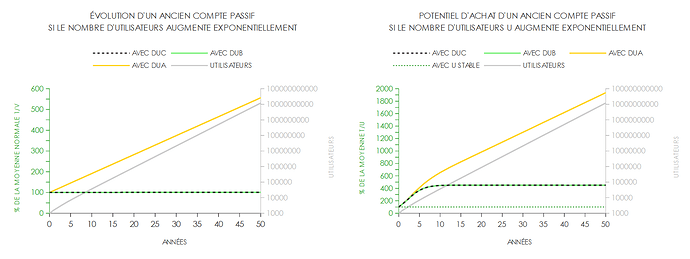
Notamment le fait que ça semble “monter” dans ce référentiel particulier (qui a une légitimité relative, comme tout référentiel), est trompeur, car ce “N” qui croît exponentiellement( jusqu’à 10¹¹ tout de même sur ton exemple, en 40 ans, soit 100 fois la population mondiale actuelle… très loin du taux de croissance humaine constaté qui a cru de quelques millions à 10⁹ en… 10 000 ans, et ne tenant pas en compte la limite de toute communauté humaine)… ce N exponentiel donc fait bien arriver des nouveaux entrants.
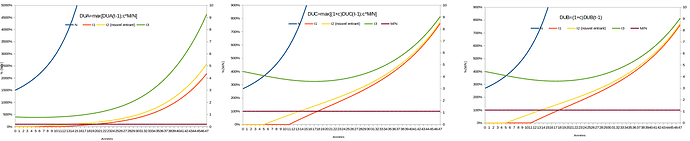
Or ces nouveaux entrants de ce N “exponentiel” verront arriver la même création monétaire que ton ancien, avec la même courbe, c’est donc l’écart qui reste stable, du fait de la variation de N dans ce cas, mais c’est vrai pour tout nouvel entrant, qui lui même devient un ancien vis à vis d’un nouveau etc… C’est dû à la réflexion particulière qui concerne justement un “N qui croît” qui est équivalent à une initialisation partielle (démarrer une monnaie revient à faire croître N de zéro à quelque chose), donc à la définition d’une valeur initiale DU(0), qu’il faut arbitrer puisque c*M/N qui est le sens fondamental pour N stable, s’effondre brusquement, que faire ?
Priviliégier les anciens = rabaisser le DU(t) à cM/N, ou privilégier les nouveaux = prendre un DU(t) > cM/N. DU(t) = DU(t-1) est donc ici un entre-deux qui a été calculé en proposition par dans la TRM (mais qui n’est pas “la TRM”), pour un taux de variation de N sur long terme correspondant à la réalité expérimentale (chacun peut le vérifier et éviter de faire dire à la TRM ce qu’elle ne dit pas… c’est une remarque générale qui ne concerne pas le sujet ici).
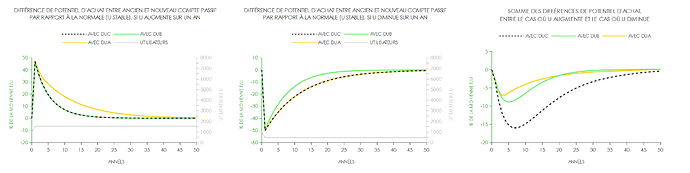
Donc tu compares deux choses très distinctes. C’est biaisé, par une comparaison inter-monnaies qui n’est pas correcte, au lieu de regarder comment les comptes évoluent les uns par rapport aux autres (relatif).
Concernant le fait de vouloir utiliser 1/c DU comme référentiel de limite à atteindre individuellement me semble pertinent et ne pas en tenir compte peut contribuer à rendre en effet les choses difficiles à expliquer, mais c’est un autre point, et il peut en effet suffire à faire un autre choix, du moment que cet autre choix varie peu.
Mais dans ce cas extrême tu dois voir que dans cet autre choix, tu ne converge pas non plus vers M/N mais bien au dessus, et ceci pour toutes les monnaies (ici N(t+1)=N(t)^(1,1))… sur 50 ans, voyez le chiffre obtenu, est-ce crédible ? DUABC.ods (104,1 Ko)
Ce qui est absolument normal.
Donc ton “potentiel d’achat” est bien supérieur à M/N quel que soit ton choix parmis DUA, DUB, et DUC, pour ce cas extrême et virtuel (jamais constaté expérimentalement, et ce pour toute espèce vivante sur Terre depuis 5 milliards d’années, pour des raisons mécaniques) de “N exponentiel fort, ici maintenant et à jamais”.
N peut être plutôt “moyennement exponentiel sur 40 ans”, avec un taux relativement faible, mais avec aussi des limites.
Penser l’infini (N qui croîtrait indéfiniment) ne semble pas compatible avec une communauté de confiance. Car comment un nombre très grand de membres, qui croîtrait indéfiniment, pourrait-il vérifier son propre nombre sans se tromper ou être trompé ? N a plus probablement une limite haute, et c’est bien ce cas de N “quasi stable”, qui est le cas central à étudier.
PS : plutôt que “compte passif” il serait plus correct de parler de “individu/compte pseudo-autonome”, car c’est équivalent à des échanges équilibrés en terme d’entrées/sorties, c’est pourquoi la TRM utilise ce terme beaucoup plus général.
Je ne comprends pas pourquoi on ne pourrait pas comparer deux espace-temps différents. Tu as choisi de représenter DUA, DUB et DUC sur des graphiques séparés mais on peut les superposer. Ce que j’ai fait revient à superposer tes graphiques : ça rend juste la comparaison plus facile.
Mes graphiques montrent que les nouveaux sont davantage privilégiés (par rapport aux anciens) avec DUA qu’avec DUB et DUC. Avec DUA, quelqu’un qui rejoint le système pendant la croissance exponentielle de N (U sur mes graphiques) a beaucoup plus de potentiel d’achat que quelqu’un qui quitte le système avant la croissance. C’est aussi vrai avec DUB et DUC mais l’écart est moins grand.
C’est ce que j’ai fait. Les courbes de droite sont relatives à M/N (T/U sur mes graphiques).
Dans mon exemple ça monte jusqu’à 12 milliards d’utilisateurs. C’est vrai que j’y ai été fort car ça dépasse la population mondiale actuelle ^^ Je vais le rendre plus réaliste. Bien sûr il ne s’agit pas ici de croissance du nombre d’être humains sur Terre, mais de croissance du nombre d’utilisateurs. Facebook est passé de zéro à 1 milliard en 10 ans. Pourquoi pas une monnaie libre ?
Oui je le vois bien, tout comme sur mes graphiques. Je vois aussi, sur mes graphiques comme sur les tiens, qu’avec DUC et DUB ça part moins haut qu’avec DUA.
Ce cas est extrême en effet et je vais le modérer un peu, mais juste un peu car je me dis qu’une monnaie libre pourrait très bien se développer de manière exponentielle sur peu d’années.
Oui je sais qu’il y a une limite. Ça se stabilisera au bout d’un moment, mais la croissance peut être forte en moyenne et durer un certain temps, c’est pourquoi je pense qu’il est intéressant d’étudier ce cas aussi.
C’est bel et bien mon critère de choix principal. C’est le point le plus important pour moi.
Le terme que tu proposes est plus général mais il ne me parle pas. Je préfère dire “compte à l’équilibre commercial”, qui me semble tout aussi exact, mais dans ma communication je dis “compte passif” en raccourci, après avoir expliqué que je le considère comme un synonyme du terme précédent… même si en réalité c’en est plutôt une sous-partie.
Sur ce qui précède, ok, si ton interprétation reste prudente et fait bien attention à ne comparer que ce qui reste comparable : écart anciens/nouveaux au sein d’une monnaie donnée (de code donné) relativement à ce même écart dans une autre monnaie. Les mettre sur un même graphique présuppose un point aveugle que tu n’as pas vu je crois (cf remarque suivante).
C’est la définition du terme selon la TRM. Après tu peux définir les termes comme tu veux, mais tu ne pourras pas éviter de gros problèmes de compréhension avec ceux qui utiliseront les définitions de la TRM, tu devras expliquer en détail tes termes à chaque fois, et l’intégration de la nouvelle définition ne sera pas immédiate ni assurée. Tu peux aussi forker de langage c’est certain, d’ailleurs les “économistes” (=chamanes danseurs de la pluie) entre eux ne s’en privent pas…
Je ne suis pas sûr de plus que ce référent que tu définis ait un quelconque sens économique intra ou même inter-monnaie étant donné ce qui suit :
Le point aveugle : peux-tu rajouter selon chaque monnaie, la valeur relative de chaque Dividende à l’instant “t” ?! Que constates-tu ? Que devient ton procédé interprétatif étant donné ce constat ? Comment mettre sur un même graphe ce qui n’a pas de rapport d’échelle simple ?
Je peux seulement utiliser des termes que je peux comprendre…
Concernant le point aveugle : si je comprends bien tu me demandes de tracer, pour chaque monnaie, la courbe du DU relatif à M/N ?
Voici 3 graphiques qui ont pour but de mesurer l’écart entre les anciens et les nouveaux dans chaque monnaie. J’ai essayé de suivre tes conseils. J’utilise une simple soustraction, plutôt qu’un écart-type qui ne me permettait pas de voir qui est privilégié. J’y retrouve ce que j’avais constaté sur tes courbes : c’est dans DUC que les nouveaux sont le plus privilégiés par rapport aux anciens. Qu’en penses-tu ? Est-ce pertinent (mis à part le problème du “point aveugle” que je n’ai pas encore compris) ?
Oui c’est ça. Car ce que tu appelles “moyenne normale”, est en fait 1/c DU, car en relatif tu comptes en DU. Ce n’est pas 1/c tout seul. Sans savoir ce que “vaut un DU” tu as un référentiel biaisé pour comparer des monnaies entre elles.
Une soustraction de quoi ? Si tu comptes en relatif, tu comptes en DU. Donc sans avoir traité le point aveugle tu ne compares rien de pertinent. Tu dois compter des écarts en quantitatif, puis comparer à M/N, pour avoir in-fine une mesure relative à la masse monétaire. Seule cette mesure est invariante par changement de référentiel, pas “le nombre de DU” sans savoir la valeur relative du DU.
Je te rappelle que le DU est calculé en phase N stable par DU = c*M/N, ce qui n’est pas le cas en phase instable où il faut donc revenir à la comparaison à M/N pour chiffrer quoi que ce soit de pertinent.
Les mesures étant biaisées par le point aveugle on ne peut rien en tirer de pertinent. Tu dois compter en quantitatif et recalculer le relatif, sinon tu as une métrique parfaitement biaisée, qui ne tient pas compte du fait que N varie, et que donc le DU n’est plus pertinent en terme de mesure parce qu’il s’adapte à cette variation de manière différente du cas stable.
C’est comme si je te disais : notre unité de mesure sur une planète X est 1/40 000 000 de sa circonférence, si la planète est stable, mais il y a des moments où elle gonfle, et d’autres où elle se dégonfle. Si donc tu comptes relativement à cette mesure, tu oublies le fait qu’elle n’est pas valable vis à vis de planètes qui ne changent pas de taille, qui ont des tailles différentes, qui varient différemment etc…
Pour comparer des mesures d’objets qui varient en taille entre eux, il faut une unité de mesure qui ne soit pas définie sur la variation de ces objets. Si on considère des économies comparables, subissant des variations de N identiques, seul M/N peut servir de mesure valide, cf comparaison relative.
Sinon c’est comme si tu comparais les prix entre l’Allemagne et la France en nombre de minimum sociaux, sans te rendre compte qu’en France il vaut 10% de M/N alors qu’en allemagne il vaut 3% de M/N. Tu aurais oublié l’essentiel.
Quand j’exprime les comptes en nombre de DU par rapport à 1/c, j’ai bien conscience que ça ne représente pas toujours le potentiel d’achat. C’est juste pour comparer les chiffres que les utilisateurs verront sur leur compte. Je compare ce que verront les utilisateurs sur leur compte dans chaque monnaie.
Concernant mes calculs de potentiel d’achat, c’est autre chose et c’est vrai que je les fais à partir des comptes exprimés en nombre de DU (par rapport à la moyenne du nombre de DU… qui n’est pas toujours 1/c). Mais si je calcule le potentiel d’achat à partir des comptes exprimés en quantitatif (unités quantitatives par rapport à leur moyenne), je constate que ça me donne exactement les mêmes courbes, pour toutes les variations de N. Je n’ai pas ton niveau en maths donc j’aurais du mal à l’expliquer.
Pas forcément ! Rien n’empêche de créer un référentiel en % de M/N. Comment les utilisateurs voudront voir leur monnaie ne dépend pas de quelqu’un d’autre. S’ils décident que telle ou telle vision de leur monnaie leur semble plus convenable qu’une autre, c’est celle qu’ils utiliseront.
Dans tous les cas rien ne t’empêche donc d’exprimer à la fois tes compte en % de 1/c DU, mais en parallèle de donner aussi la valeur relative du DU en % de M/N qui subira des variations avec N.
Ce n’est pas difficile à expliquer :
Si N varie peu le DU vaudra quelque chose de proche de son état fondamental = c*M/N et donc la monnaie vaudra quelque chose proche de M/N = 1/c DU.
En cas de variations fortes de N le DU subira des variations différentes selon la formulation choisie pour DU(t), mais les comptes convergeront à moyen - long terme de manière sensiblement équivalente dans la très grande majorité des cas où ces variations resteront bornées, ceci conformément à l’expérience des communautés humaines et conformément aux règles de limites imposées par la Toile de Confiance (TdC en Français, ou bien WoT en anglais pour Web of Trust).
A l’aide de graphiques bien choisis on peut donc montrer précisément ces points en n’oubliant pas de montrer selon les cas, la variation relative du DU qui ne sera donc pas la même.
Ce qui suffit comme explication générale. Ensuite pour être précis il faut passer par des comparaisons de calculs définis, qui demandent de ne comparer que ce qui est comparable entre plusieurs monnaies (cf M/N).
Ça dépend de comment est fait le logiciel. Les concepteurs du logiciel peuvent très bien choisir de mettre en avant l’affichage en % de 1/c DU.
J’ai choisi de mettre en parallèle les comptes en % de 1/c DU et les comptes en % de M/N (= potentiel d’achat des comptes). Est-il vraiment nécessaire d’ajouter la valeur du DU en % de M/N ? Ça me semble contenu dans le potentiel d’achat des comptes…
Le principe du libre c’est que tout reste facilement modifiable. Il n’y a donc rien de particulièrement “mis en avant”
Dans ce cas non, tout y est. Mais ce n’est pas une question d’affichage. C’est une question de comparaison entre codes ici.
L’affichage est anecdotique.
Je mettrai probablement en avant les comptes en % de 1/c DU, tant pis si ça empêche mon logiciel d’être libre. Je veux simplifier les choses au maximum afin que ce soit accessible à tout le monde.
Si tu utilises Duniter, tu ne pourras pas empêcher le logiciel d’être libre, il sera forcément libre.
Puisque je ne veux pas utiliser la formule DUA, je n’utiliserai probablement pas Duniter.
Sauf à ce qu’il existe un autre logiciel similaire dont j’ignore l’existence, tu préférerais donc ne pas du tout utiliser de monnaie libre simplement parce que la tête de la formule ne te plaît pas ?
Adapter Duniter pour prendre une autre formulation du DU est possible.
