Proposition for changing the distance rule

[cgeek]

OK, so this is a big topic . A little disclaimer:

I would be very grateful if you guys interested in uCoin protocol, tell me what you think about it.

Thanks!

---

We used to talk a lot about Sybil attack & distance rule with a lot of controverse & passion. This leads me today to tell you I want to radically change this rule and enumerate the reasons why below, along with the new form I want to give it and I could call statistical distance rule.

Just to avoid you reading the whole post to know what is the new rule I propose, here it is:

Statistical distance rule is the rule that considers a member to be at a max distance k from any other member if it is certified by enough unique members in its first s steps, with s [1;k] and k being the maximum diameter of the web-of-trust.

Or differently said:

If an identity has enough unique certifiers in its first s steps, then we can consider the member will be at a distance k from almost all the members of the WoT.

So, with k = 5 and s = 3 distance rule, the member will be accepted in a WoT of diameter k = 5 if he has at least u unique certifiers in its s = 3 first steps, u value being given by a formula.

So the whole WoT won’t be checked to accept the member. That’s why I call it statistical distance rule: because the distance is not hardly checked, but deduced from statistics.

Note: we use indifferently k to refer to the maximum WoT size and to the maximum distance between 2 parts of the WoT, or two parts in an hypothetic WoT. The reason is: the definition of the diameter is that any part (any member, node or whatever synonym we use to designate a vertex) a has a maximum distance k with any other part of the WoT.

If you want to dive into the details, please read the following paragraphs.

The current distance rule

How it works

Currently, the distance rule is processed the following way:

• when an identity joins or renews, it is checked against the WoT rule
• the identity must match the distance rule with each sentry of the WoT, that is all the members with at least sigWoT valid certifications to them
• for each sentry:
  • try to find a path from the sentry to the identity by using at most stepMax steps
  • if no path exist, the identity does not match the distance rule

The computation problem

The whole problem in this algorithm is scalability. Indeed, finding a path is a hard problem, and in the worst case (when no path actually exists) we have to go through almost all the WoT.

While this isn’t a big problem for 1.000 members, 100.000 members with 10 certifications each makes a lot of computation. Imagine: we might have to test all the links of 5 steps of a 100k members WoT for each sentry and for each newcomer/renewer, each time we receive a block with identities in it.

Given the fact we would like uCoin to be run by low machine peers, this might not be an acceptable algorithm. I thought it could work, but the more I dig in the more pessimist I am. Maybe it exists some trick that could make it easy to compute, but I havn’t found it yet.

Also, as I often say, I am not building an Airbus nor a Boeing. I just want something that flies. If I can use a cheaper solution (both in computing & time development cost), I will certainly prefer it. Today, I am looking at the better trade-off to have something that works for 100.000 members (if more, that would be a bonus), yet I don’t want to delay again and again the launch of a beta currency.

That’s why I propose you statistical distance rule.

The possible attacks

Not only the current rule is a hard computation problem, it is also vulnerable to an attack shared by @Arcurus.

To avoid it, we must alter the distance rule to something like:

The distance rule have to apply to at least 90% of the sentries

instead of 100% of them. Even with this, we are not fully protected against the attack (I let you dig in the above link for more details).

The new rule

Abstract

Considering what we want is to roughly have a maximum diameter k for the WoT, because we understood that:

• it may exists individuals at an infinite distance (if they do not certify anyone)
• we can’t have the rule applied continuously (the distance rule is applied against the WoT, so the WoT cannot be tested against itself, we have to consider only “externalities” against it: the newcomers/renewers)

We understand that it can be acceptable to have a rule that statistically leads to a WoT of max diameter k.

The perfect tree of k diameter

First of all, let’s define what we call a perfect tree of k diameter.

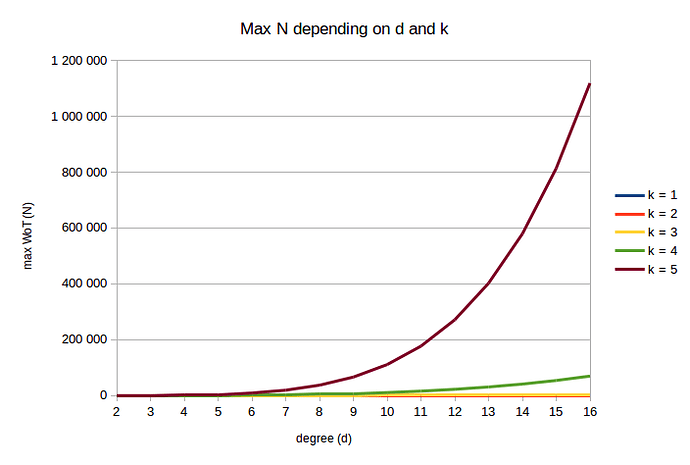
Imagine a tree where each member appears only once, for a newcomer. A perfect tree of degree d = 2 would be able to define this newcomer by 2 previous members, themselves being certified by 2 previous members, and so on until step k. So for a diameter k = 3 we have exactly:

$$N = 2^0 + 2^1 + 2^2 + 2^3 = 1 + 2+ 4 + 8 = 15$$ members.

Generalizing with degree d

Exact value

We cannot generalize this rule by an inequality with any value of d (this is a sum of successive powers of a same basis d, which apparently is an unsolved problem). Instead, we can use a table of value telling us what is the link between d, k and perfect tree N using the formula:

$$(a)$$ $$N = \sum\limits_{i=0}^k d^i$$

d	k = 1	k = 2	k = 3	k = 4	k = 5
2	3	7	15	31	63
3	4	13	40	121	364
4	5	21	85	341	1 365
5	6	31	156	781	3 906
6	7	43	259	1 555	9 331
7	8	57	400	2 801	19 608
8	9	73	585	4 681	37 449
9	10	91	820	7 381	66 430
10	11	111	1 111	11 111	111 111
11	12	133	1 464	16 105	177 156
12	13	157	1 885	22 621	271 453
13	14	183	2 380	30 941	402 234
14	15	211	2 955	41 371	579 195
15	16	241	3 616	54 241	813 616
16	17	273	4 369	69 905	1 118 481

Which gives us the following graph:

Approximation

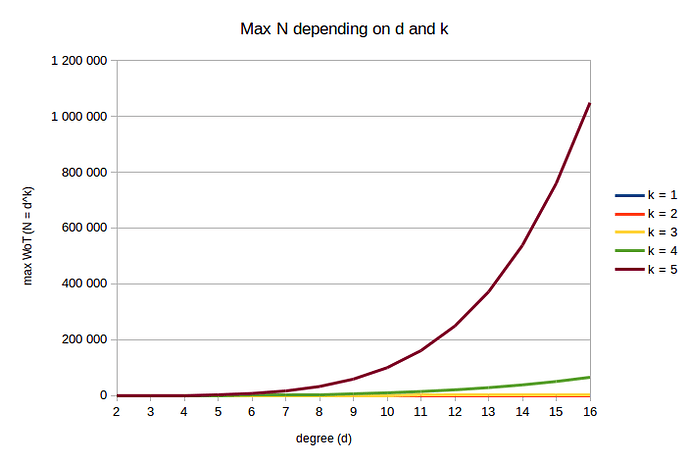
For the purpose of uCoin, we could use an approximation of (a) which would be:

$$(b)$$

$$ N = d^k $$

Which gives us the following table:

d	k = 1	k = 2	k = 3	k = 4	k = 5
2	2	4	8	16	32
3	3	9	27	81	243
4	4	16	64	256	1 024
5	5	25	125	625	3 125
6	6	36	216	1 296	7 776
7	7	49	343	2 401	16 807
8	8	64	512	4 096	32 768
9	9	81	729	6 561	59 049
10	10	100	1 000	10 000	100 000
11	11	121	1 331	14 641	161 051
12	12	144	1 728	20 736	248 832
13	13	169	2 197	28 561	371 293
14	14	196	2 744	38 416	537 824
15	15	225	3 375	50 625	759 375
16	16	256	4 096	65 536	1 048 576

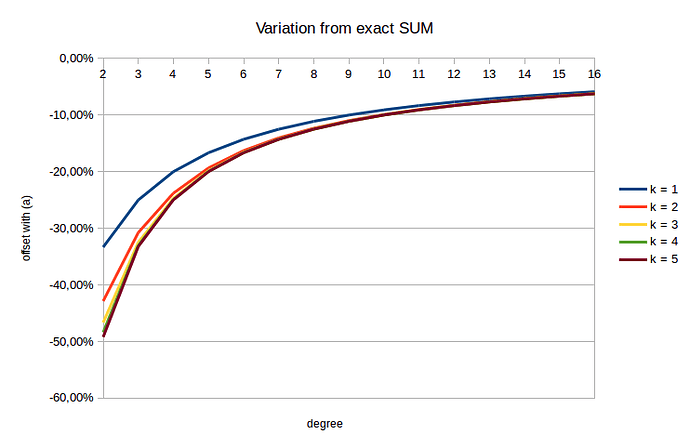
We can see the distribution is amlost the same as with (a) formula. Here is the difference:

d	k = 1	k = 2	k = 3	k = 4	k = 5
2	-33,33%	-42,86%	-46,67%	-48,39%	-49,21%
3	-25,00%	-30,77%	-32,50%	-33,06%	-33,24%
4	-20,00%	-23,81%	-24,71%	-24,93%	-24,98%
5	-16,67%	-19,35%	-19,87%	-19,97%	-19,99%
6	-14,29%	-16,28%	-16,60%	-16,66%	-16,66%
7	-12,50%	-14,04%	-14,25%	-14,28%	-14,28%
8	-11,11%	-12,33%	-12,48%	-12,50%	-12,50%
9	-10,00%	-10,99%	-11,10%	-11,11%	-11,11%
10	-9,09%	-9,91%	-9,99%	-10,00%	-10,00%
11	-8,33%	-9,02%	-9,08%	-9,09%	-9,09%
12	-7,69%	-8,28%	-8,33%	-8,33%	-8,33%
13	-7,14%	-7,65%	-7,69%	-7,69%	-7,69%
14	-6,67%	-7,11%	-7,14%	-7,14%	-7,14%
15	-6,25%	-6,64%	-6,66%	-6,67%	-6,67%
16	-5,88%	-6,23%	-6,25%	-6,25%	-6,25%

So we see that, the more the degrees, the less the difference there is between (a) and (b). Also, the distance k does not affect much the result but on the early stages of the WoT where d \leq 5.

However the usage of this formula (b) allows us to determine d_{min} from any N:

(c)

$$ d_{min} = \exp{(\frac{\ln{(N)}}{k})} $$

Which gives the following values:

This graph actually shows how much N is reachable given each member has d_{min} certifications to him in the WoT of max diameter k.

Notable results for the perfect WoT (perfect tree of the WoT):

• requires d = 16 certifications per member to reach N = 1.118.481 in a WoT of k = 5 diameter
• requires d = 32 certifications per member to reach N = 1.118.481 in a WoT of k = 4 diameter

Of course, uCoin won’t deal with a perfect WoT. We will discuss this point later in this post.

The acceptable heuristic

My proposal is actually very simple:

When a newcomer/renewer comes in, if its first steps (k - 1 steps) lead to at least u = d_{min}^{k - 1} unique certifiers, then we agree that statistically he will be at a distance k from any other member of the WoT.

Did not get it? I just mean that if by checking the certifications, direct or indirect, at 1,2,3 and 4 steps from you we have enough unique certifiers, then we could accept to say you are at distance 5 from any other member.

Generalizing with s steps

We can generalize this rule by replacing k - 1 by s:

When a newcomer/renewer comes in, if its first steps (s steps) lead to at least u = d_{min}^s unique certifiers, then we agree that statistically he will be at a distance k from any other member of the WoT.

Of course, the lower the value of s, the easier it is for eventual cheaters to create fake accounts.

Some values

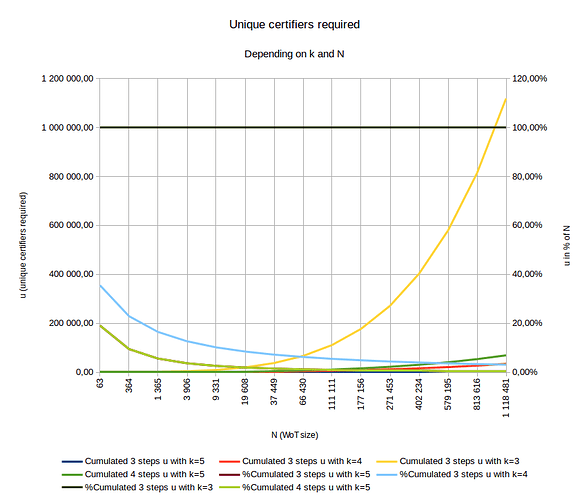
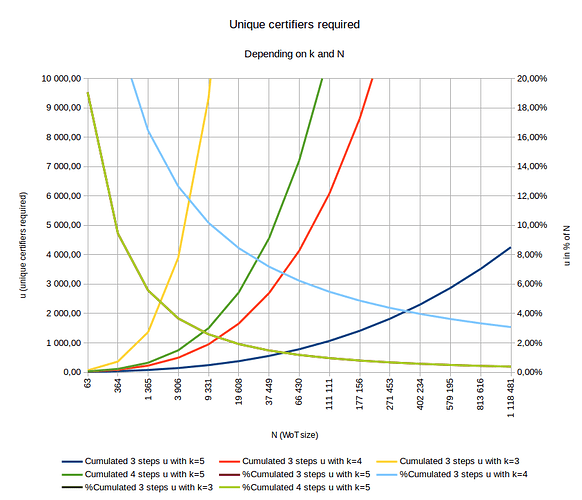
Here is a graph summing up values of u according to N (N is the size of the WoT when the individual comes in or renew) and k the max diameter of the WoT:

and the same graphe with a closer view:

• The growing curves are quantitative values of u
• The shrinking curves are relative values of u (relative to N)
• 2 curves have exactly the same values:
  • %Cumulated 3 steps u with k = 5
  • %Cumulated 4 steps u with k = 5

My wish for a WoT with k = 5 would be to have either:

• s = 4 so we check only the first 4 steps of any newcomer:
  \rightarrow means to find ~100.000 unique certifiers in a WoT of ~1.000.000 members (red curve)

• s = 3 so we check only the first 3 steps of any newcomer:
  \rightarrow means to find ~4.200 unique certifiers in a WoT of ~1.000.000 members (blue curve)

I would prefer s = 3 for performance reasons.

The real WoT is not a perfect tree

Of course, the real, in-production web-of-trust won’t be a perfect tree.

As a rule of thumb, we could imagine an almost perfect tree to be contained in a tree of double size of the perfect tree.

This is pure speculation, I don’t know what value would be correct. But I need to go on, so I propose 2 because obviously it needs to be \gt 1, and 2 means that statistically one of two certifications we made can reach a k steps individual. This does not shock me, even if I really prefer to have real numbers to verify this assertion.

If we take the rule of double-size, this means members will require, statistically, the double quantity of certifications to reach maximized N.

In a WoT(k = 5), this means people will require to have at least d_{min} \times 2 = 16 \times 2 = 32 certification stock.

Link with other parameters

According to above result, if we also consider the following rules:

• certification expiry: each cert expires after 1 year
• certification replay: each cert can be replayed (from A to B) 5 years after expiry date

… a community aiming at reaching N = 1.000.000 individuals permanent size with k=5 must have constantly 32 cert by individual/year, so each individual must have 32 \times (5 + 1) = 192 directly known individuals over 5 + 1 = 6 years, which is rougly 3 individuals a month.

This results seems acceptable to me.

We finally have to consider the certification delay rule, which says “an individual can make a certification every X days”.

Given above values, X have to be \lt 365,25 / 32 = 11,41 days.

If we want some margin with certification stock, and put it to 60 for example, we will have to adapt certification delay rule value accordingly: X \lt 365,25 / 60 = 6 days.

Remarkable cases

s = k

This means any member must be directly connected to any member. This is a very strong rule, and will lead to blocking cases if a member refuses to certify individuals.

Even worse, an individual who do not certify anyone will have the power of death over the WoT as long as he stays to be a member.

That’s why, in reality, it is wisheable to have s \lt k.

s = k = 1

This is pure trust distance rule: every member directly signs each other member.

Consequences

Implementing such a rule would lead to:

• Removal of sigWoT parameter
• Add s parameter
• Enventually add a p factor, to say the threshold to reach u_{threshold} = p \times u. So we can say “each member has to reach at least p times the theoretical value of unique certifiers”.

So on the implementation side, the rule is rather simple. Finding the unique certifiers are a one shot SQL query, but the higher s and N the more complex is the query in terms of execution.

Now I am waiting for your comments.

Thanks for reading.

---

Please find LibreOffice Calc file from which I’ve made the graphs: Statisitcal_distance.ods (93.2 KB)

More links:

• Table of the largest known graphs of a given diameter and maximal degree - Wikipedia
• Distance (graph theory) - Wikipedia

[s_b_]

Thanks for this proposition,
What is exactly a “sentry” ? ;o

[cgeek]

I edited the main post to give a link to the definition.

You can find it here: sentry.

[Galuel]

“Imagine: we might have to test all the links of 5 steps of a 100k members WoT for each sentry and for each newcomer/renewer, each time we receive a block with identities in it.”

• It is not sure there is not an algorithm to do it quickly for a max number of 10 000 000 members for instance
• It is also possible to compute this at a specific frequency, for instance every 10 days or every 40 days, and not doing it for “every block”. So the computation can be much more easier.

[Inso]

@Galuel

It is not sure there is not an algorithm to do it quickly for a max number of 10 000 000 members for instance

I think this problem is like the Floyd Warshall algorithm. Its complexity is O(n^3).

[Galuel]

@Inso

Its complexity is O(n^3).

It can be O(n³), and can be solved in 30 secs for 10 000 000 members. that is to say for 100 000 000 members it will be solved in 30 secs x (100 000 000)³ / (10 000 000)³ = 30 secs x 1000 = 8h33

So without knowing the time necessary to solve it for a number, we cannot conclude, if there is a good solution for 1000 000 members for instance, which can be enough to know.

[cgeek]

@Galuel

It is not sure there is not an algorithm to do it quickly for a max number of 10 000 000 members for instance

OK, I will make tests with Floyd Warshall algorithm, and also with Dijkstra’s algorithm.

The tests will consist in a random distribution of 16 links per member, with 1.000.000 members. And test roughly 2% (this is worldwide birth rate) random members for distance.

I will be able then to make the links vary in quantity and also the quantity of members.

@Galuel

It is also possible to compute this at a specific frequency, for instance every 10 days or every 40 days, and not doing it for “every block”. So the computation can be much more easier.

The problem is not the frequency of the block, but the frequency of the newcomers/renewers. Each generates a distance test against the WoT.

Also, the cost is in the extraction of the links to create a WoT matrix that can be computed in-memory.

Finally, the current rule still have a big problem as an attack has been described here. So the current distance rule cannot be applied to the whole WoT at any time, but a part of it.

[Inso]

Maybe you could use networkx to do so (or maybe I could, since I already know the library).

This library can

• Generate graph automatically : http://networkx.github.io/documentation/networkx-1.10/reference/generators.html

• And use multiple shortest path algorithms : http://networkx.github.io/documentation/networkx-1.10/reference/algorithms.shortest_paths.html

As it is implemented in python, it’s not like ucoin nodes, but it’s not too far for it probably.

[cgeek]

Well I planned to use C code, both for fun and because we do not exactly need shortest path, but just to know if at least one path exists.

This is probably easier challenge than shortest path.

[Inso]

In the worst case, its complexity is the same as the shortest path, thought.

[Galuel]

@cgeek

The problem is not the frequency of the block, but the frequency of the newcomers/renewers. Each generates a distance test against the WoT.

What I said is still available. You can have a test every n days, and so a newcomer has to wait the next WoT test to be fully in, I don’t see any problem for that. So you don’t need to calculate at a frequency you don’t control.

@cgeek

Finally, the current rule still have a big problem as an attack has been described here.

There are rules solutions for that. For instance, to be a member in the links calculation, you need to have minimum a recursive link with Dmax path. So this attack cannot occur with that rule.

[cgeek]

@Galuel

For instance, to be a member in the links calculation, you need to have minimum a recursive link with Dmax path.

Could you explain a bit more?

[Galuel]

The problem of this attack is to block expansion of the WoT by limitation. To be a member you need at least a Dmax path to at least another member. So you cannot have members with all link paths < Dmax

[Galuel]

Another rule can be : Sum(from path=1 to path=2) of all linked people >= 100. So you don’t need 100 people directly, but 10x10, is much more to control indirectly. And so you cannot have a WoT < 100(2 paths), and that sibyll attack with 4 people cannot occur.

Generally, what could be usefull to help other contributors to think about the WoT rules, would be to propose different images with definition of the constants, and time history events in WoT(t) and WoT(t+dt) illustrating some problems, and what is happening. With only text it is not easy to “see” what is happening.

[cgeek]

@Galuel

Sum(from path=1 to path=2) of all linked people >= 100. So you don’t need 100 people directly, but 10x10, is much more to control indirectly.

Ok so this is my rule with s=2. I think it’s good.

[Arcurus]

to the complexity and ram use:
For a single joiner / re-newer the complexity to check if he reaches all or x% of sentries in distance n is O(n).
the trick is to check all sentries on the same run.

Here the algorithm:
list a = empty
list b = new member to check

for i=1 to maxdistance
a = b
b = empty

do while a not empty
Take m = the first member from list a
remove m from a

for each certification c of m
if c.issuer is not marked then mark c.issuer and put in list b
loop
loop

the memory per member with average certifications per member <10 is around 10 * 8 bytes (64 bit pointer).
so lets say 100 bytes. With 1 GB ram we should therefore be able to handle 1.000.000.000 /100 = 10 million people.
that looks ok for the beginning

later on if needed we could also fragment the members in groups as abstraction.

for example one group contains all members that fulfill the WOT rules to members of this group with max distance d1

each group trusts all groups that one single member of this group trusts.

on the second level the WOT is tested for each group equally handled like member wot is handled with max distance d2

because we know that each member is in max distance d1 to each member of this group and because we know each group is of max distance to each group of d2, we know that the wot d1 + d1+d2 <= dmax is fulfilled on a global scale.

[Arcurus]

@Galuel

There are rules solutions for that. For instance, to be a member in the links calculation, you need to have minimum a recursive link with Dmax path. So this attack cannot occur with that rule.

this would only increase the count of attackers from 4 to Dmax+1, therefore is no true solution for this attack.

@Galuel

Sum(from path=1 to path=2) of all linked people >= 100

this solution is better, but increases the count of attackers to 100.
an better solution like suggested in the attack topic is to require to reach x% lets say 3/4 of the sentries to become a sentry
and to require for a newcomer to only reach x% lets say 3/4 of the sentries.

another solution would be to count only both way certifications as true trust relations.
of course both solutions could be combined

[Galuel]

@Arcurus

another solution would be to count only both way certifications as true trust relations.of course alwaysboth solutions could be combined

Yes, It seems a nice combined solution because of symmetrical and scalable properties.

There is a point to think about : proportions are not always the way to obtain a good scalable law, it depends many times of the subject. I’m not sure a proportional law (x%) is the most precise one concerning graphs.

[Arcurus]

@Galuel

Yes, It seems a nice combined solution because of symmetrical and scalable properties

yea, i think it would solve many problems and would make the need of sentries obsolete.
The only situation which remains is what to do if the web of trust is broken.

In this case the above outlined solution to require only X% of members could be a good solution.
A more ¨strict¨ solution would be to count which of the broken WOT parts has more members.
The new WOT is then the biggest.

@Galuel

There is a point to think about : proportions are not always the way to obtain a good scalable law, it depends many times of the subject. I’m not sure a proportional law (x%) is the most precise one concerning graphs.

Just to have an example to better understand the implications: In a way the WOT could be looked at as an liquid democracy with (currently) only positive votes / delegations (vote / delegation = certification) and where the max distance of your delegated vote is dmax.

Currently you need the vote of 100% of the sentries to be in, therefore one sentry is enough to block all newcomers / renewers
With 3/4% of the votes 1/4 of the sentries could block a newmember, or the other way round you need 3/4 of all sentries votes to join / renew your membership.

[cgeek]

Both way certifications are a wrong good idea, since it would alter the motivation of certifying someone (do I certify him because I checked its identity, or do I do it to pass the both ways rule?) and change the meaning of the certifying act: someday it means A (I checked its identity), some day it means B (I want a both ways path), some other day A and B.

uCoin certification meaning today is unequivocal: I trust this identity to exist and represent only human in the currency.

If you give two meanings to a certification, then the WoT won’t have any meaning at all.