Étude de la WoT

Galuel · 14 June 2016 11:44

En essayant d’utiliser les noms des variables tels que définies dans le code, afin d’uniformiser.

Règles en français avec noms des variables.

Etant donné que les certifications ont une limite maximale d’expiration dans le temps sigValidity (par exemple 1 an), et une limite basse entre deux certifications sigPeriod (par exemple 1 semaine), le nombre maximal de certifications que l’on peut émettre est :

sigValidity / sigPeriod = 52 / 1 = 52

Le stock maximal de certification sigStock est donc inférieur ou égal à ce maximum technique. Pourquoi pas égal !?

sigStock = sigValidity / sigPeriod

Des études ont montré que des palliers remarquables en terme d’organisation sont 12, 50 et 150 personnes, des nombres comme 20, 70 ou 200 se ramènent à ces palliers en terme de fonctionnement.

On sait à peu près que les économies dynamiques sont celles de pays de tailles moyennes (Pays-Bas, Suisse, Nouvelle Zélande), de quelques millions de membres au plus.

Y[N] correspond au nombre de signatures à émettre pour être “sentry” = point de contrôle, il dépend du nombre de membres maximal N. Etant donné qu’on a un diamètre maximal de la toile = maxstep, on obtient facilement que, au plus :

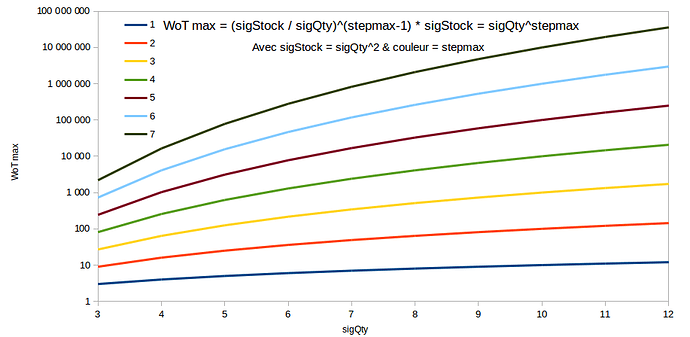
Y[N] = N^(1/maxstep) ou encore que N = Y[N]^maxstep

Or donc Y[N] sera inférieur ou égal au maximum de signatures possibles, et si on prend le pallier de 50 comme base de persones connues et “fonctionnant bien ensemble”, et maxstep = 4 qui est un nombre de pas expérimentalement correct on aura :

N = Y[N]^maxstep = 50^4 = 6 250 000

Qui correspond à peu près à l’ordre de grandeur recherché.

Mais on ne peut pas atteindre ce nombre théorique si le nombre de signatures requises pour devenir membre sigSty est plus grand que 1, car à chaque pas, ce n’est pas une signature qui sera consommée par membre mais au moins sigSty. De plus tous les membres ne signeront pas le maximum d’autres membres, mais ce sont les “sentry” qui en feront le plus.

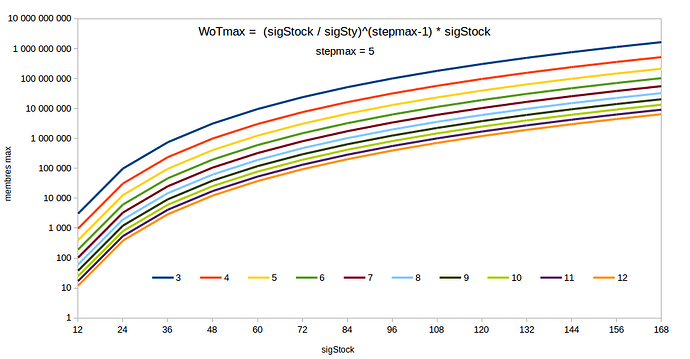
Si donc on veut prétendre pouvoir atteindre, en pratique, ce niveau, alors il vaut mieux avoir un stock de signatures possibles bien supérieur sigStock = Y[N] x sigSty

Etant donné le pallier de 150, et Y[N] = 50 ça ferait un sigSty = 3 ce qui semble peu… Mais ensuite on a du mal à imaginer beaucoup de points de contrôles avec plus de 150 connaissances… Il faut donc réduire Y[N], ce qui revient à soit baisser la valeur maximale de N soit augmenter maxstep.

Si on considère que maxstep = 4 est déjà fort, alors on va limiter N et choisir Y[N] plus faible. Avec Y[N] = 42, on aura un bon score à plus de 3 millions de membres possibles.

Résumons, de bonnes valeurs semblent donc être :

maxstep = 4
sigSty = 4
Y[N] = N^(1/maxstep) = 42 (bon chiffre !)
N (max théorique) = Y[N]^maxstep = 3 111 696
sigStock = sigValidity / sigPeriod = Y[N] x sigSty = 168
sigPeriod = 1 semaine => sigValidity = Y[N] x sigSty x sigPeriod = 168 semaines = 3 ans + 3 mois

A noter que sigStock et sigValidity ne sont donc pas véritablement des paramètres mais des calculs forcés tirés des autres paramètres.

Si on considère que maxstep peut être augmenté tout en baissant Y[N], par exemple à Y[N] = 12, et pour garder un maximum théorique de 3 millions, alors maxstep = ln(N)/ln(Y[N]) = 6. Dans ce cas on pourrait avoir les paramètres suivants :

maxstep = 6
Y[N] = N^(1/maxstep) = 12
N (max théorique) = Y[N]^maxstep = 2 985 984
sigSty = 12
sigStock = sigValidity / sigPeriod = Y[N] x sigSty = 144
sigPeriod = 1 semaine => sigValidity = Y[N] x sigSty x sigPeriod = 144 semaines = 2 ans et 10 mois

A noter que si on veut un renouvellement annuel avec une certification hebdomadaire, alors on limite forcément sigStock à 52, et donc dans ce dernier cas Y[N] = sigStock / sigSty = 8 et N (max) = Y[N]^maxstep = 262 144.

En se rappelant notamment qu’il faut signer des membres chaque semaine, sans en laisser passer pour atteindre ce max. On comprend donc par ce raisonnement que sigValidity et sigPeriod déterminent fortement l’expansion maximale de la WoT, et qu’il vaut mieux calibrer un N max théorique bien supérieur à celui qui est visé.

Avec maxstep = 4, sigStock = 48, sigSty = 6 :

maxstep = 4
Y[N] = sigStock/sigSty = 8
N (max théorique) = Y[N]^maxstep = 4096
sigSty = 6
sigStock = sigValidity / sigPeriod = Y[N] x sigSty = 48
sigPeriod = 1 semaine => sigValidity = Y[N] x sigSty x sigPeriod = 48 semaines

Galuel · 15 June 2016 08:57

Il y a une approximation dans l’approche sur le nombre certifiable. Il faut revoir ce point avec précision pour bien maîtriser ces paramètres et mieux savoir ce qu’ils permettent d’envisager.

Imaginons que nous ayons une sphère 1 de sigStock membres, ils possèdent donc globalement sigStock² signatures, permettant ainsi la signature de sigStock² / sigQty membres (dont les sigStock membres initiaux font partie). Ex : avec sigStock = 150 et sigQty = 12 => 1875 membres potentiels >> 150

Il reste donc au delà des SigStock membres initiaux : sigStock² / sigQty - sigStock = sigStock (sigStock/sigQty - 1) membres possibles.

Si on veut donc aller au delà du premier cercle pour que la WoT augmente il faut donc sigStock/sigQty> 1 => Voilà déjà une première condition fondamentale.

sigStock/sigQty > 1 (note : 50/12 > 1 et 150/12 > 1)

Ces nouveaux membres sont potentiellement déjà à une distance de 2 d’au moins 1 point de contrôle de la première sphère. Combien voulons-nous qu’ils soient, potentiellement, pour que la progression ne soit pas bridée jusqu’à stepmax ?

La progression maximale est en proportion de très exactement sphère2 / sphère1 : (sigStock² / sigQty) / sigStock = sigStock / sigQty, idem pour la sphère 3, la sphère 4 etc.

Donc la sphère n maximale sera de taille : (sigStock / sigQty)^(n-1) * sigStock

Avec n = stepmax on obtient donc la taille maximale théoriquement autorisée :

taille WoT max = (sigStock / sigQty)^(stepmax-1) * sigStock

WoT max fonction de sigStock en abscisse et sigQty en couleur de barre pour stepmax = 4 :

Tableur : WoTmax.ods (64,6 Ko)

Avec stepmax = 5 :

Tableur : WoTmax.ods (26,2 Ko)

Avec sigStock = sigQty^2 => WoT max = (sigStock / sigQty)^(stepmax-1) * sigStock = sigQty^stepmax

Tableur : WoTmax.ods (19,8 Ko)

cgeek · 15 June 2016 10:32

Je partagerai mon analyse plus tard, mais mais voici quelques commentaires.

Définition : `Y[N] = sigStock/sigQty` = levier

On voit ce rapport sigStock/sigQty un peu partout, et si je devais lui donner un nom ce serait “levier” d’ajout de membres par membre.

Ça correspond au fait que chaque membre possède un stock sigStock de certifications qu’il peut émettre au maximum, couplé au fait que pour être membre lui-même, il y a nécessairement sigQty certifications autres que les siennes qui ont été consommées à son bénéfice.

On peut prendre l’exemple d’un groupe d’individus faisant monnaie ensemble et requérant 3 certifications pour être membre (sigQty = 3) : il faut a minima 4 membres émettant chacun 1 certification pour chaque autres membre, donc chaque membre émet 3 certifications pour les autres.

On comprend bien que si sigStock = sigQty, alors on a un levier unitaire : on ne dispose pas de certifications pour faire entrer des membres supplémentaires, le groupe restera à 4 membres au plus, et ne pourra d’ailleurs pas faire moins sans tomber à une toile vide du fait de sigQty = 3 qui expulse tous les membres dès qu’un des 4 tombe.

Mais si sigStock = 6 et sigQty = 3, alors on a un levier de 6/3 = 2 : chaque membre permet l’existence de 2 membres dans la toile, dont lui-même + 1 supplémentaire. Ce qui rejoint ta 1ère conclusion :

Remarque 1)

En fait je me demande si, en ayant sigStock membres initiaux > sigQty + 1, on ne serait pas déjà dans un cas à 2 cercles, le 2ème cercle étant constitué de sigStock - (sigQty + 1) membres.

C’est toi-même qui me l’a fait remarqué ici : https://logs.duniter.org/duniter/2016-05-18/#12:20:53, et je pense, à raison.

Et donc si l’on reconsidère le cas de la sphère 1, elle serait plutôt constituée de sigQty + 1 membres. On dispose donc de (sigQty + 1) * sigStock certifications initiales, permettant de signer (sigQty + 1) * sigStock / sigQty membres. Pour reprendre l’exemple ça donnerait : sigStock = 150 et sigQty = 12 => 162.5 membres potentiels.

Galuel · 15 June 2016 10:53

Ce n’est pas le cas étudié. Le cas étudié recherche un max, et donc suppose au moins un membre ayant signé le maximum de membres soit sigStock. Ce membre étant “sentry” c’est lui qui limite la sphère 1, par la distance 1. Au delà on entre dans la distance 2 donc la sphère 2. L’étude ici étudie comment la WoT s’étend step by step (sphère par sphère) relativement à ce sentry. Ce qui est commode pour trouver ce max.

Par ailleurs le fait qu’on ait sigstock membres initiaux (en fait sigstock + 1 si on compte le sentry, mais c’est négligeable) ne préjuge pas qu’on en ait plus, mais on compte les signatures disponibles et on voit jusqu’où on peut aller pour le step 2, et on raisonne par récurrence.

A noter que Il vaut mieux parler de sphère pour la WoT, puisque ce qui est valable pour un membre, peut être valable pour tout autre membre, ce qui est valable pour une sphère où les points sont indifférenciés, mais pas pour des disques par exemple, puisque le centre est un point spécial.

On doit donc imaginer les membres de la WoT comme étant placés sur une sphère. Les sphères 1, sphère 2… sphère n peuvent être vues comme une même sphère, où les membres sont de plus en plus nombreux (et de plus en plus éloignés - en terme de distance de graphe - relativement à au moins 1 sentry initial, on pourrait donc les voir dans des couleurs différentes en fonction du niveau de sphère considéré).

Exemple avec sigStock = 3 et admettons ici stigQty = 1, tous les membres possibles n’y sont pas, mais les distances y sont, 3 sphères visibles : Sphere 1 = vert, Sphere 2 = vert + orange, Sphere 3 = vert+orange+rouge. C’est bien une question de distance.

cgeek · 15 June 2016 11:44

OK, mais dans ce cas pour clarifier on pourrait utiliser Ninit comme nom de variable pour le nombre de membres de la sphère 1, si effectivement le nombre de membres initiaux est arbitraire dans l’étude et peut donc être différent de sigStock ou même différent de sigQty + 1…

De cette façon on obtient :

taille WoT max = (sigStock / sigQty)^(stepmax-1) * Ninit

Et alors on comprend que la taille max de la WoT est facteur de ce nombre, changeant, et peut aller du simple au double, au triple, au décuple … et repousse à lui seul (si le raisonnement est juste), dynamiquement, la taille max de la WoT en référence aux sphères relatives au membre étudié.

Galuel · 15 June 2016 11:45

Et il vaut combien au maximum “Ninit” pour définir la première distance = 1 !? A noter qu’une fois la WoT lancée, tout membre remplissant la condition maximale qui existera pourra être utilisé pour le calcul. “Ninit” n’est pas un nombre qui dépend de “t=0”…

cgeek · 15 June 2016 14:31

Je raisonnais en considérant une sphère “pseudo-isolée”, c’est-à-dire une sphère dont les individus sont signataires les uns des autres et qui reste stable, comme l’est nécessairement une toile initiale qui prétend passer de t0 à t1 sans s’effondrer. D’où mon idée de “Ninit” qui réfère aux membres initiaux.

Edit : D’ailleurs je me rends compte pourquoi je perds le fil du raisonnement, tu car tu dis : “dont les sigStock membres initiaux font partie”, ce qui m’embrouille. Pas besoin de dire initiaux, ce sont juste les “sigStock membres”. Ou alors je n’ai rien compris

Mais tu peux aussi considérer toute sphère possible, notamment la sphère avec un max de membres. Ça me va, continuons.

Sinon, +1 pour ton 1er post. Je le comprends d’autant mieux que je remplace “Y[N]” par “levier”.

cgeek · 15 June 2016 14:53

Non vraiment ce passage n’est pas clair, je ne comprends pas. Si quelqu’un ayant compris pouvait reformuler svp …

Galuel · 15 June 2016 15:01

8 membres ayant sigStock = 8 signatures chacun ont en tout 8² = 64 signatures. Ils peuvent donc avec sigSty = 2 signer en tout 8²/2 = 32 membres, dont eux-mêmes = 8 membres initiaux (ce qui fait 32 - 8 = 24 membres supplémentaires possibles).

cgeek · 15 June 2016 15:17

Oui d’accord, mais pourquoi pas 10 membres ayant un stock de 8 signatures chacun ?

Galuel · 15 June 2016 15:24

A cause de la distance. Si tu en as 10 tu es déjà forcément dans la sphère 2 avec au moins 2 membres distants de 2.

Avec 8 (en fait 8+1 = 9 pour être précis), tu peux être dans la sphere 1 MAX. Or on cherche le max, donc on cherche à remplir au maximum toutes les spheres jusqu’à stepmax.

cgeek · 15 June 2016 16:54

Oui OK on cherche effectivement à la remplir pour produire la plus grande toile possible, sphères suivantes incluses et dépendantes de la sphère précédente.

C’est bon, j’ai compris.

Galuel · 15 June 2016 17:39

Si donc on veut plus de précision, il faut donc rajouter +1 qui correspond à notre sentry de départ = Sphere(0) (un seul membre), ce qui ne change pas grand chose à quelques % près puisqu’on comprend vite qu’il faudra dans tous les cas très certainement sigStock > 50

Sphere(n) = (sigStock+1)*(sigStock / sigQty)^(n-1)
Sphere(stepmax) = (sigStock+1)*(sigStock / sigQty)^(stepmax-1)

L’étude des graphes ci-dessus (et des tableurs adaptés) permettront donc de choisir de bons paramètres en fonction de la WoT visée, on choisira une WoT(stepmax) plus grande.

cgeek · 15 June 2016 19:15

WoT plus grande oui, mais dans quel ordre de grandeur ? 2x plus ? 5x plus ? 10x plus ?

Galuel · 15 June 2016 19:51

Rien du tout… Pour sigStock = 50, ça fait au plus 2% par step (en fait moins). Pour 4 steps : (1,02)^4 = 1,08, c’est 8% de plus. Pour SigStock plus grand c’est encore moins. C’est négligeable c’est pour ça que je ne l’ai pas mis au départ. Ca n’a vraiment pas grand intérêt…

Il suffit de regarder la fonction pour le voir. Si on est pas convaincu => tableur.

Inso · 16 June 2016 05:26

J’ai pris le temps de relire tout ça 2-3 fois pour m’assurer de bien comprendre. J’ai encore quelques questions :

Sur la première partie

Y[N] est bien l’équivalent du tableau des signatures requises pour devenir sentry que cgeek avait calculé ? Pourquoi calculer Y[N] fonction de stepmax et ne pas reprendre le tableau de cgeek ?

Sur la deuxième partie

J’en conclu que plus la WoT possède de sentries, plus son diamètre est limité ?
Pourquoi 8 membres initiaux ? C’est ici un cas avec sigQty = 1 ?

Je ne vois pas d’ou vient le chiffre “2% / step” dans l’étude. La question de cgeek portait sur le taille de la WoT max à calculer en fonction de la WoT visée, j’ai l’impression que tu lui as répondu sur l’impact des sentries de départ sur la taille max ?

Pour finir

L’étude est très intéressante, on arrive enfin à un calcul précis pour déterminer le max. On va pouvoir pondérer quel paramètre impacte le plus sur la taille max finale.
Ensuite, nous pourrons analyser l’impact de chaque paramètre sur la fragilité de la WoT par rapport à l’attaque des sybils, et on pourra alors, je pense, commencer à déterminer des paramètres idéaux pour une WoT de production.

L’image de la sphère pour “voir mentalement” la WoT c’est très bien aussi. C’est effectivement beaucoup plus clair dans mon esprit, sur comment observer la WoT.

A noter que en parallèle, simuler des WoT reste pertinent car ça permet de réaliser des éléments importants. Par exemple, si il y a trop de monde à vouloir rejoindre la WoT, et que les certifications se dispersent de trop entre les membres et les individus en attente d’entrée, la WoT ne peut pas grandir. (Phénomène reproduit sur les simulations de greyzlii, cgeek et moi). L’impact est qu’il faut que les logiciels guident l’utilisateur dans l’exercice de certification, sans pour autant le faire à leur place

Très de bavardages, je continue de lire la suite de l’étude avec intéret en tout cas.

Galuel · 16 June 2016 07:00

Le tableau repose sur quel calcul ? Il est clair que Y[N] est bien en rapport avec N et stepmax (au moins, puisque stigStock le limite aussi), il faut donc établir une bonne fonction de calcul de Y[N], et ne pas prendre de nombres au hasard ou dans une liste arbitraire.

Comme les sentries sont ceux qui signent le plus, ce sont eux qui vont déterminer le diamètre de la WoT(max) au plus proche.

Comme on veut qu’en plus ils signent un maximum possible de membres dans la WoT max, on obtient aussi :

Y[Nmax] = SigStock/sigQty

Or (sigStock+1)*(sigStock / sigQty)^(stepmax-1) = Sphere(stepmax) = Nmax

D’où Y[Nmax] = [Nmax/(sigStock+1)]^[1], qui est proche de Nmax^(1/stepmax)

A noter que pour Nmax = 10 000 000 et sigStock = 150, stepmax = 4, on obtient Y[N] = 40 et sigQty = 3 ce qui expérimentalement semble concorder (un bon moyen de savoir si une formulation a de bonnes chances d’être correcte, c’est de vérifier que les chiffres obtenus dans des cas un peu connu semblent corrects).

Si on prend Y[Nmax] = Nmax^(1/stepmax) on obtient pour le même cas Y[Nmax] = 25 et sigQty = 6, ce qui semble plus sûr pour l’acceptation d’un membre.

Non. Démonstration : stepmax = 2, sigStock = 8, sigQty = 2 et Y[N] = 8, 8^2/2 = 32 membres possibles, il peut y avoir 32 sentries possibles, ça ne limite pas le diamètre. S’il n’y en a aucun, il n’y aura pas 32 membres mais moins, puisque alors 7^2 / 2 => 24 membres possibles au maximum.

Après si on prend Y[N] = N^(1/stepmax), pour 10 membres ont a Y[10] = 3, on peut avoir 0 sentry.

C’est un calcul de maximum, pas un calcul quelconque. C’est 8+1 membres initiaux pour Sphere(1) si on veut être précis. Car le sentry max (duquel on part pour calculer) signe ici 8 membres. Au delà de ces 8 nous entrons dans la Sphere(2). Le calcul du max se fait ici par raisonnement par récurrence sur les Sphere(n) pour voir quel maximum on peut atteindre pour chacune d’entre elles jusqu’à la dernière = Sphere(stepmax).

Dans l’exemple pour sigStock = 50, rajouter 1 revient à rajouter 2% à stigStock. Quand on compare ensuite les deux formulations :

(A) Sphere(n) = (sigStock+1)*(sigStock / sigQty)^(n-1)
(B) Sphere(n) = (sigStock)*(sigStock / sigQty)^(n-1)

Pour sigStock = 50, A/B =1 + 2%, d’ailleurs ça ne joue même pas à chaque step, le terme de droite étant inchangé. C’est donc simplement (A) qu’il faut prendre, et (A) ne diffère de (B) que faiblement. J’aurais mieux fait d’être précis dès le départ, car je constate que ça rajoute du texte dans le fil pour rien du tout…

Quand on se lance dans du calcul d’ordre de grandeur on fait ça à peu près à la louche… Après on peut préciser, c’est mieux…

On peut aussi voir les sphères imbriquées les unes dans les autres (comme les poupées russes), ce qui est visuellement pratique pour bien voir les distances et identifier les chemins rapidement.

C’est le sens de l’issue sur sakia et cesium.

1/(stepmax-1) ↩︎

cgeek · 16 June 2016 07:40

Je me suis mal exprimé : je parlais du fait que, mettons qu’on souhaite à terme atteindre une WoT de 1M (1.000.000) de membres par le jeu des certifications moyennes. Doit-on viser les paramètres pour une WoT à 2M ? 5M ? 10M ?

Galuel · 16 June 2016 07:55

Le max ne sera pas atteint, car il faut utiliser toutes les signatures + les renouveler en permance n’oublions pas… + éviter de sur-signer des membres déjà actifs (ce que ne manqueront pas de faire la plupart des membres…), pour ne pas perdre de stock de signatures.

C’est donc complexe de savoir ce qu’il faut viser car le comportement des hommes sur ce sujet est complètement inconnu il faut bien le savoir, il n’y aucun exemple vérifiable. Mais je dirais au pif au moins 10 Millions, et peut-être même très certainement 100 millions.

Ils nous disent que la moyenne de liens sociaux est de 50 (pas 150 qui est plutôt un max), si donc on se base sur les mêmes calculs avec 50 et stepmax = 4, avec sigQty = 5

Sphere(stepmax) = (50+1)*(50 / 5)^3 = 51 000, on ne va pas bien loin…
WoTmax = (150+1)*(150/5)^3 = 4 077 000 soit 80 fois plus

Avec stepmax = 5 :

Sphere(stepmax) = (50+1)*(50 / 5)^4 = 510 000 c’est mieux
WoTmax = (150+1)*(150/5)^4 = 122 310 000 soit 240 fois plus

Ce tout petit essai montre bien comment la WoTmax ne fait que très largement encadrer la WoT visée… Mais là en sus je n’ai pas fait le calcul des liens entre Y[N] sigStock etc… Il faut donc réaliser une étude numérique précise à partir des formulations données plus haut.

cgeek · 16 June 2016 08:00

C’est l’un des trucs assez fort de raisonner en “max” : Galuel n’a pas du tout besoin de connaître le tableau que j’ai produit, et même mieux : il peut me dire si les valeurs que j’ai prises sont cohérentes ou non.

Si je les reprends (je rappelle que ce ne sont que des points particuliers, il existe une courbe générale) :

N         Y(N)  
10        2  
100       4  
1000      6  
10000     8  
100000    12  
1000000   20

Je dirais que ça reste cohérent en termes de grandeurs avec ce qu’il a trouvé, en ce qu’il s’agit du nombre minimum pour être point de contrôle. Mais on peut aussi décider qu’il faille avoir une courbe plus proche du max afin de n’avoir des contraintes de distance que pour ceux où il existe un maximum de chemins, donc ayant émis le plus de certifications possibles.